题目内容
(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答只以甲题计分)
甲:设数列{bn}的前n项和为Sn,且bn=2-Sn;数列{an} 为等差数列,且a5=9,a7=13.
(Ⅰ)求数列 {bn} 的通项公式;
(Ⅱ)若cn=anbn(n=1,2,3,…),Tn为数列{cn}的前n项和,求Tn.
乙:定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
-
(a∈R)
(Ⅰ)求f(x)在[0,1]上的最大值;
(Ⅱ)若f(x)是[0,1]上的增函数,求实数a的取值范围.
甲:设数列{bn}的前n项和为Sn,且bn=2-Sn;数列{an} 为等差数列,且a5=9,a7=13.
(Ⅰ)求数列 {bn} 的通项公式;
(Ⅱ)若cn=anbn(n=1,2,3,…),Tn为数列{cn}的前n项和,求Tn.
乙:定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
| 1 |
| 4x |
| a |
| 2x |
(Ⅰ)求f(x)在[0,1]上的最大值;
(Ⅱ)若f(x)是[0,1]上的增函数,求实数a的取值范围.
甲:(Ⅰ)由bn=2-Sn,令n=1,则b1=2-S1,∴b1=1,…(1分)
当n≥2时,由bn=2-Sn,可得bn-bn-1=-(Sn-Sn-1)=-bn,…(3分)
∴bn=
bn-1,…(4分)
∴数列{bn}是以1为首项,
为公比的等比数列
∴bn=
.…(6分)
(Ⅱ)数列{an}为等差数列,公差d=
(a7-a5)=2,∴an=2n-1,…(8分)
从而cn=anbn=(2n-1)•
,…(9分)
∴Tn=1+
+…+(2n-1)•
∴
Tn=
+
+…+(2n-3)•
+(2n-1)•
两式相减可得:
Tn=1+
+
+…+
-(2n-1)•
=3-
…(11分)
从而Tn=6-
.…(12分)
乙:(Ⅰ)设x∈[0,1],则-x∈[-1,0],∴f(-x)=4x-a•2x
∵f(-x)=-f(x),∴f(x)=a•2x-4x,x∈[0,1],…(3分)
令t=2x,则t∈[1,2],∴g(t)=at-t2=-(t-
)2+
∴当
≤1,即a≤2时,g(t)max=g(1)=a-1;
当1<
<2,即2<a<4时,g(t)max=g(
)=
;
当
≥2,即a≥4时,g(t)max=g(2)=2a-4;.…(8分)
(Ⅱ)因为函数f(x)在[0,1]上是增函数,
所以f′(x)=2xln2(a-2•2x)≥0 …(10分)
∴a≥2•2x恒成立
∵x∈[0,1]
∴a≥4 …(12分)
当n≥2时,由bn=2-Sn,可得bn-bn-1=-(Sn-Sn-1)=-bn,…(3分)
∴bn=
| 1 |
| 2 |
∴数列{bn}是以1为首项,
| 1 |
| 2 |
∴bn=
| 1 |
| 2n-1 |
(Ⅱ)数列{an}为等差数列,公差d=
| 1 |
| 2 |
从而cn=anbn=(2n-1)•
| 1 |
| 2n-1 |
∴Tn=1+
| 3 |
| 2 |
| 1 |
| 2n-1 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
两式相减可得:
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 22 |
| 2 |
| 2n-1 |
| 1 |
| 2n |
| 2n+3 |
| 2n |
从而Tn=6-
| 2n+3 |
| 2n-1 |
乙:(Ⅰ)设x∈[0,1],则-x∈[-1,0],∴f(-x)=4x-a•2x
∵f(-x)=-f(x),∴f(x)=a•2x-4x,x∈[0,1],…(3分)
令t=2x,则t∈[1,2],∴g(t)=at-t2=-(t-
| a |
| 2 |
| a2 |
| 4 |
∴当
| a |
| 2 |
当1<
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
(Ⅱ)因为函数f(x)在[0,1]上是增函数,
所以f′(x)=2xln2(a-2•2x)≥0 …(10分)
∴a≥2•2x恒成立
∵x∈[0,1]
∴a≥4 …(12分)

练习册系列答案
相关题目
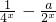 (a∈R)
(a∈R) 只以甲题计分)
只以甲题计分)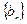 的前
的前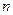 项和为
项和为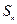 ,且
,且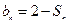 ;数列
;数列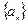 为等差数列,且
为等差数列,且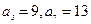
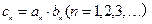 ,
,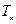 为数列
为数列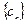 的前
的前 项和,求
项和,求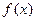 ,已知当
,已知当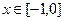 时,
时,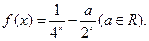
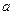 的取值范围
的取值范围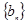 的前
的前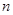 项和为
项和为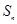 ,且
,且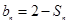 ;数列
;数列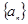 为等差数列,且
为等差数列,且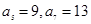
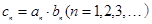 ,
, 为数列
为数列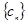 的前
的前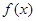 ,已知当
,已知当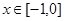 时,
时,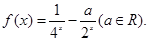
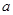 的取值范围
的取值范围