题目内容
(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
甲:设数列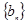 的前
的前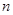 项和为
项和为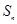 ,且
,且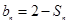 ;数列
;数列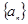 为等差数列,且
为等差数列,且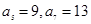
(Ⅰ)求数列 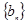 的通项公式
的通项公式
(Ⅱ)若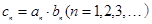 ,
, 为数列
为数列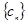 的前
的前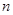 项和,求
项和,求
乙:定义在[-1,1]上的奇函数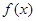 ,已知当
,已知当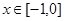 时,
时,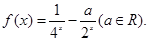
(Ⅰ)求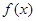 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若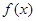 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数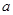 的取值范围
的取值范围
【答案】
甲:解:(Ⅰ)由 ,…1分
,…1分
 , ………3分
, ………3分
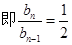 ,
…………………4分
,
…………………4分
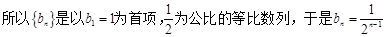 .……6分
.……6分
(Ⅱ)数列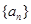 为等差数列,公差
为等差数列,公差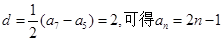 ,……8分
,……8分
从而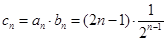 ,
…………………………9分
,
…………………………9分
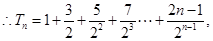
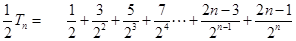
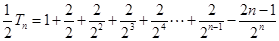
=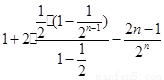
=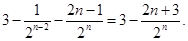 ………………………………………11分
………………………………………11分
从而 .…………………………………12分
.…………………………………12分
乙:乙:解:(Ⅰ)设 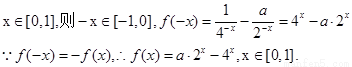 ……3分
……3分
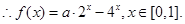 …………5分
…………5分
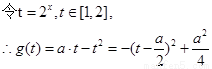
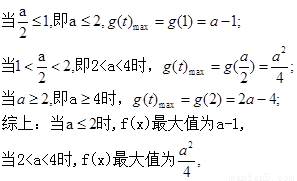
当a≥ 4时,f(x )的最大值为2a-4. …………8分
(Ⅱ)因为函数f(x)在[0,1]上是增函数,
所以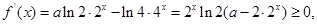 …………10分
…………10分
 …………12分
…………12分
【解析】略

练习册系列答案
相关题目