摘要:18. 如图.A.B两点之间有6条网线并联.它们能通过的最大信息量分别为1.1.2.2.3.4.现从中任取三条网线且使每条网线通过最大的信息量. (I)设选取的三条网线由A到B可通过的信息总量为x.当x≥6时.则保证信息畅通.求线路信息畅通的概率, (II)求选取的三条网线可通过信息总量的数学期望. 解: (I) (II) ∴线路通过信息量的数学期望 答:(I)线路信息畅通的概率是. (II)线路通过信息量的数学期望是6.5.
网址:http://m.1010jiajiao.com/timu3_id_4464229[举报]
(本小题满分12分)
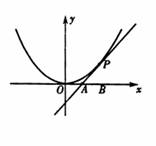 如图,已知直线l与抛物线
如图,已知直线l与抛物线![]() 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
(I) 若动点M满足![]() ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
查看习题详情和答案>>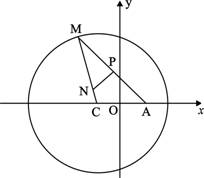 (本小题满分12分) 如图所示,已知圆
(本小题满分12分) 如图所示,已知圆![]() 为圆上一动点,点
为圆上一动点,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且满足
上,且满足![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率为k的动直线
且斜率为k的动直线![]() 交曲线
交曲线![]() 于A、B两点,在y轴上是否存在定点G,满足
于A、B两点,在y轴上是否存在定点G,满足![]() 使四边
使四边
形![]() 为矩形?若存在,求出G的坐标和四边形
为矩形?若存在,求出G的坐标和四边形![]() 面积的最大值;若不存
面积的最大值;若不存
在,说明理由。
查看习题详情和答案>>
 及
及 ACB=
ACB= ,求A、B两点间的距离,以及
,求A、B两点间的距离,以及
 及
及 ACB=
ACB= ,求A、B两点间的距离,以及
,求A、B两点间的距离,以及