题目内容
(本小题满分12分)已知函数f(x)＝kx3－3(k＋1)x2－2k2＋4，若f(x)的单调减区间为(0,4)．
(1)求k的值；
(2)对任意的t∈[－1,1]，关于x的方程2x2＋5x＋a＝f(t)总有实根，求实数a的取值范围．
【答案】
解：(1)f′(x)＝3kx2－6(k＋1)x，
又∵f′(4)＝0，∴k＝1.
(2)由(1)得f(x)＝x3－6x2＋2，
∴f′(t)＝3t2－12t.
∵当－1<t<0时，f′(t)>0；当0<t<1时，f′(t)<0，且f(－1)＝－5，f(1)＝－3，
∴f(t)≥－5.
∵2x2＋5x＋a≥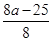
，
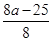∴≤－5，解得a≤－
.
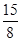【解析】略
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
