Question

(本小题满分12分)   已知函数f(x)＝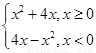

(1)作出函数的图像简图，并指出函数的单调区间；

（2）若f(2－a²)>f(a)，求实数a的取值范围.

 

Answer 1

【答案】

(1) f(x)在(－∞，＋∞)上是单调递增函数；（2）－2<a<1.

【解析】本试题主要是考查了函数的 图像，以及函数的单调性和解不等式的总额和运用。

（1）先由已知解析式作出图像，然后根据图像得到单调区间，进而得到。

（2）在第一问的基础上可知，哈双女户得 单调性质，f(x)在(－∞，＋∞)上是单调递增函数，然后结合单调性得到结论。

解析：(1) 略          ………………………………………………………………4分

由f(x)的图象可知f(x)在(－∞，＋∞)上是单调递增函数，……………………7分

（2）由（1）可知f(x)在(－∞，＋∞)上是单调递增函数

故由f(2－a²)>f(a)得2－a²>a，即a²＋a－2<0，…………………………………10分

解得－2<a<1.…………………………………………………………………………12分