摘要：20．本题共有2个小题.第1小题满分4分.第2小题满分10分. 根据指令.机器人在平面上能完成下列动作:先原地旋转角度(为正时.按逆时针方向旋转.为负时.按顺时针方向旋转-).再朝其面对的方向沿直线行走距离. (1)现机器人在直角坐标系的坐标原点.且面对轴正方向.试给机器人下一个指令.使其移动到点(4.4). (2)机器人在完成该指令后.发现在点处有一小球正向坐标原点作匀速直线滚动.已知小球滚动的速度为机器人直线行走速度的2倍.若忽略机器人原地旋转所需的时间.问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位). [解](1) [解](2)
网址：http://m.1010jiajiao.com/timu3_id_4463816[举报]
(本小题满分14分)
设
椭圆方程为
抛物线方程为
如图4所示，过点
作
轴的平行线，与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
（1）求满足条件的椭圆方程和抛物线方程；
（2）设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得
为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标) 。
(本小题满分14分)设b>0，椭圆方程为
，抛物线方程为
.如图4所示,过点F(0,b+2)作x轴的平行线，与抛物线在
第一象限的交点为G.已知抛物线在点G的切线经
过椭圆的右焦点
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点，试探究在
抛物线上是否存在点P，使得△ABP为直角三角形？
若存在，请指出共有几个这样的点？并说明理由
（不必具体求出这些点的坐标）.
查看习题详情和答案>>本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
如图，已知正方体
的棱长为2，
分别是
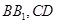的中点．
（1）求三棱锥
的体积；
（2）求异面直线EF与AB所成角的大小（结果用反三角函数值表示）．
查看习题详情和答案>>
．
的解集；
的三边
，
，
满足
，且边
，求角
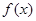的值域．
椭圆方程为
抛物线方程为
如图4所示，过点
作
轴的平行线，与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标) 。