摘要:22.本题共有3个小题.第1小题满分5分.第2小题满分6分.第3小题满分7分. 已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T.对任意x∈R.有f(x+T)=T f(x)成立. (1)函数f(x)= x 是否属于集合M?说明理由, (2)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点.证明: f(x)=ax∈M, (3)若函数f(x)=sinkx∈M ,求实数k的取值范围. 普通高等学校招生全国统一考试 数学答案
网址:http://m.1010jiajiao.com/timu3_id_4463732[举报]
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数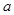 的值;
的值;
(3)在(2)的条件下,是否存在实数 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设数列 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.
查看习题详情和答案>>
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
查看习题详情和答案>>
 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为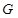 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数