题目内容
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数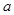 的值;
的值;
(3)在(2)的条件下,是否存在实数 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(1)当 时,总有
时,总有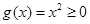 满足①……………………………1分
满足①……………………………1分
当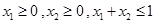 时,
时,
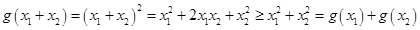 满足②………3分
满足②………3分
所以函数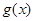 为
为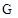 函数;………………………………………………………4分
函数;………………………………………………………4分
(2)因为函数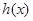 是
是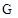 函数,根据①有
函数,根据①有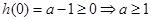 ,……………6分
,……………6分
根据②有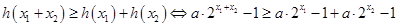
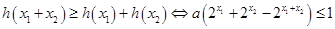
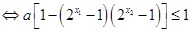 …………………………………………………7分
…………………………………………………7分
因为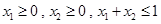 ,
,
所以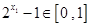 ,
,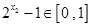 ,其中
,其中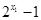 和
和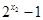 不能同时取到
不能同时取到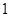 ,
,
于是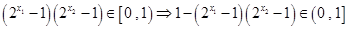 ,……………………9分
,……………………9分
所以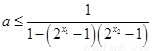 ,即
,即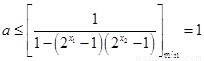 ,……………10分
,……………10分
于是 …………………………………………………………………………11分
…………………………………………………………………………11分
另解:因为函数 是
是 函数,根据①有
函数,根据①有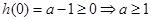 ,…………6分
,…………6分
根据②有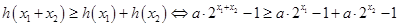
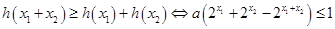 ………………………………8分
………………………………8分
取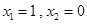 得
得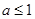 …………………………………………………………10分
…………………………………………………………10分
于是 …………………………………………………………………………11分
…………………………………………………………………………11分
(3)【理科】根据(2)知 ,原方程可以化为
,原方程可以化为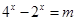 ,……………12分
,……………12分
由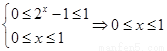 ,……………………………………………………14分
,……………………………………………………14分
令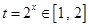 ,则
,则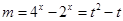 ,………………………………………15分
,………………………………………15分
由图形可知:当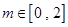 时,方程有一解;…………………………………16分
时,方程有一解;…………………………………16分
当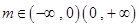 时,方程无解;…………………………17分
时,方程无解;…………………………17分
因此,方程不存在两解。………………………………………………………18分
【文科】根据(2)知 ,原方程可以化为
,原方程可以化为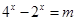 ,…………………12分
,…………………12分
由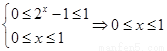 ,……………………………………………………14分
,……………………………………………………14分
令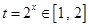 ,…………………………………………………………………15分
,…………………………………………………………………15分
则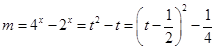 ,……………………………………………16分
,……………………………………………16分
因此,当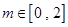 时,方程有解。……………………………………………18分
时,方程有解。……………………………………………18分
【解析】略

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案 本题共3个小题,第1、2小题满分各5分,第3小题满分6分.
本题共3个小题,第1、2小题满分各5分,第3小题满分6分. 的前
的前 项和为
项和为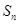 ,若对任意的
,若对任意的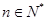 ,有
,有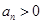 且
且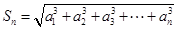 成立.
成立. 、
、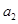 的值;
的值;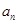 ;
;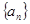 的前
的前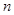 项和为
项和为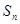 ,令
,令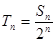 ,若对一切正整数
,若对一切正整数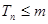 ,求
,求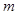 的取值范围.
的取值范围.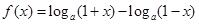
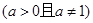
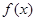 的奇偶性与单调性;
的奇偶性与单调性;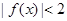 的解集为
的解集为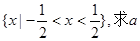 的值;
的值;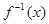 ,若关于
,若关于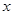 的不等式
的不等式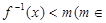 R)有解,求
R)有解,求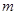 的取值范围.
的取值范围.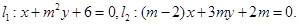 讨论当实数m为何值时,(1)
讨论当实数m为何值时,(1)