题目内容
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
解(1)∵f(x)是定义域为R的奇函数,
∴f(0)=0, …………………… 2分
∴1-(k-1)=0,∴k=2, …………………… 4分
(2)(文)
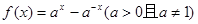
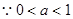 ,
,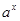 单调递减,
单调递减,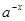 单调递增,故f(x)在R上单调递减。
单调递增,故f(x)在R上单调递减。
…………………… 6分
原不等式化为:f(x2+2x)>f(4-x)
∴x2+2x<4-x,即x2+3x-4<0 …………………… 8分
∴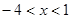 ,
,
∴不等式的解集为{x|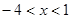 }. …………………………10分
}. …………………………10分
(2)(理)
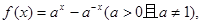
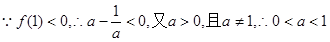 ………………6分
………………6分
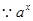 单调递减,
单调递减,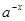 单调递增,故f(x)在R上单调递减。
………………7分
单调递增,故f(x)在R上单调递减。
………………7分
不等式化为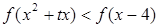
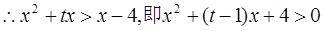 恒成立,…………… 8分
恒成立,…………… 8分
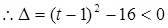 ,解得
,解得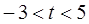 。…………………… 10分
。…………………… 10分
(3)∵f(1)=,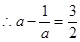 ,即
,即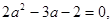
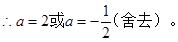 ……………………………………12分
……………………………………12分
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x为增函数
∵x≥1,∴t≥f(1)=,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥)………………15分
若m≥,当t=m时,h(t)min=2-m2=-2,∴m=2………… 16分
若m<,当t=时,h(t)min=-3m=-2,解得m=>,舍去……17分
综上可知m=2. ………………………………18分
【解析】略

 53随堂测系列答案
53随堂测系列答案 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成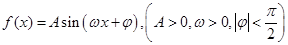 的图象的一部分如下图所示。
的图象的一部分如下图所示。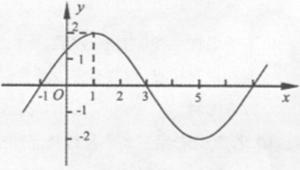
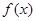 的解析式;
的解析式;
 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.