摘要：17．解:(1)取BC.C1C的中点分别为H.N.连结HC1. 连结FN.交HC1于点K.则点K为HC1的中点.因 FN//HC.则△HMC∽△FMK.因H为BC中点 BC=AB=2.则KN=.∴ 则HM=.在Rt△HCC1.HC2=HM·HC1. 解得HC1=.C1C=2. 另解:取AC中点O.以OB为x轴.OC为y轴.按右手系建立空间坐标系.设棱柱高为h.则C.F().D().E.∴.由CF⊥DE.得.解得h=2. (2)连CD.易得CD⊥面AA1B1B.作DG⊥AF.连CG. 由三垂线定理得CG⊥AF.所以∠CGD是二面角C-AF-B 的平面角.又在Rt△AFB中.AD=1.BF=1.AF=. 从而DG=∴tan∠CGD=. 故二面角C-AF-B大小为arctan.
网址：http://m.1010jiajiao.com/timu3_id_4463182[举报]
选考题请从下列三道题当中任选一题作答，如果多做，则按所做的第一题计分，请在答题卷上注明题号．
22-1设函数f（x）=|2x-1|+|2x-3|
（1）解不等式f（x）≤5x+1；
（2）若g(x)=
| 1 | ||
|
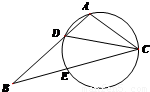
22-2如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC，
（1）求证：BE=2AD；
（2）当AC=1，BC=2时，求AD的长．
22-3已知P为半圆C：
|
| π |
| 3 |
（1）求以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．
选考题
请从下列三道题当中任选一题作答，如果多做，则按所做的第一题计分，请在答题卷上注明题号．
22-1设函数f（x）=|2x-1|+|2x-3|
（1）解不等式f（x）≤5x+1；
（2）若
定义域为R，求实数m的取值范围．
22-2如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC，
（1）求证：BE=2AD；
（2）当AC=1，BC=2时，求AD的长．
22-3已知P为半圆
上的点，点A的坐标为（1，0），O为坐标原点，点M在射线OP上，线段OM与半圆C上的弧AP的长度均为
（1）求以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．
查看习题详情和答案>>
请从下列三道题当中任选一题作答，如果多做，则按所做的第一题计分，请在答题卷上注明题号．
22-1设函数f（x）=|2x-1|+|2x-3|
（1）解不等式f（x）≤5x+1；
（2）若
定义域为R，求实数m的取值范围．22-2如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC，
（1）求证：BE=2AD；
（2）当AC=1，BC=2时，求AD的长．
22-3已知P为半圆
上的点，点A的坐标为（1，0），O为坐标原点，点M在射线OP上，线段OM与半圆C上的弧AP的长度均为（1）求以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．
查看习题详情和答案>>
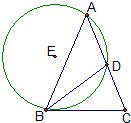（1）如图，在△ABC中，AB=AC，∠C=72°，⊙E过A，B两点且与BC相切于点B，与AC交于点D，连接BD，若BC=| 5 |
（2）过点A（2，3）的直线的参数方程为
|
（3）若关于x的不等式x+|x-1|≤a无解，则实数a的取值范围为
A．已知方程|2x-1|-|2x+1|=a+1有实数解，则a的取值范围为[-3，-1）
[-3，-1）
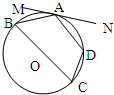
．B．如图，四边形ABCD内接于⊙O，BC是直径，MN切⊙O于A，∠MAB=25•，则∠D=
115°
115°
．C．设曲线C的参数方程为
|
|
4
4
．
在A，B，C，D四小题中只能选做2题，每题10分，共计20分．A、如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE=BE，E在BC上．求证：PE是⊙O的切线．
B、设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
（1）求矩阵M的特征值及相应的特征向量；
（2）求逆矩阵M-1以及椭圆
| x2 |
| 4 |
| y2 |
| 9 |
C、已知某圆的极坐标方程为：ρ2-4
| 2 |
| π |
| 4 |
（Ⅰ）将极坐标方程化为普通方程；并选择恰当的参数写出它的参数方程；
（Ⅱ）若点P（x，y）在该圆上，求x+y的最大值和最小值．
D、若关于x的不等式|x+2|+|x-1|≥a的解集为R，求实数a的取值范围． 查看习题详情和答案>>