题目内容
 A.已知方程|2x-1|-|2x+1|=a+1有实数解,则a的取值范围为
A.已知方程|2x-1|-|2x+1|=a+1有实数解,则a的取值范围为[-3,-1)
[-3,-1)
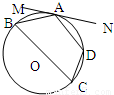
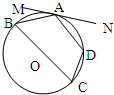
.B.如图,四边形ABCD内接于⊙O,BC是直径,MN切⊙O于A,∠MAB=25•,则∠D=
115°
115°
.C.设曲线C的参数方程为
|
|
4
4
.分析:A.若方程|2x-1|-|2x+1|=a+1有实数解,实数a+1应该属于函数y=|2x-1|-|2x+1|的值域,我们结合绝对值函数在定区间上的值域求法,易得函数y=|2x-1|-|2x+1|的值域,进而得到实数a的取值范围.
B.观察要求的角,包括两部分即∠ADB和∠BDC,根据同弧所对的圆周角和弦切角相等,得到∠ADB的度数,根据要求的角包含的另一部分是直径所对的圆周角,得到结果.
C.由题意曲线C的参数方程是:
(θ为参数),
,然后两个方程两边平方相加,即可求解;然后找出圆心和半径,构造直角三角形,从而求出弦长.
B.观察要求的角,包括两部分即∠ADB和∠BDC,根据同弧所对的圆周角和弦切角相等,得到∠ADB的度数,根据要求的角包含的另一部分是直径所对的圆周角,得到结果.
C.由题意曲线C的参数方程是:
|
|
解答: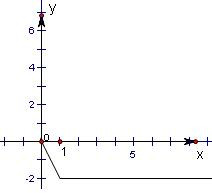 解:A.设y=|2x-1|-|2x+1|,再令2x=t,则y=|t-1|-|t+1|,(t>0),其图象如图所示,
解:A.设y=|2x-1|-|2x+1|,再令2x=t,则y=|t-1|-|t+1|,(t>0),其图象如图所示,
∴-2≤y<0,
由方程|2x-1|-|2x+1|=a+1有实数解
∴-2≤a+1<0,
∴-3≤a<-1
故实数a的取值范围[-3,-1).
故答案为:[-3,-1)
B.连接BD,AC,根据弦切角定理∠MAB=∠ACB=∠ADB=25°
∵∠D所对的弧是
,
∴∠D=∠ADB+∠BDC
∴所求角度为25°+90°=115°
故答案为:115°
C.∵曲线C的参数方程是:
,(θ为参数),
∴(x-2)2+(y+1)2=9,
∴圆心0为(2,-1),半径r=3,
直线l的参数方程为
(t为参数),它的普通方程为:x-2y+1=0,
∵曲线C被直线l所截,
∴圆心到直线的距离为:d=
=
,
∴弦长=2×
=4,
故答案为:4.
 解:A.设y=|2x-1|-|2x+1|,再令2x=t,则y=|t-1|-|t+1|,(t>0),其图象如图所示,
解:A.设y=|2x-1|-|2x+1|,再令2x=t,则y=|t-1|-|t+1|,(t>0),其图象如图所示,∴-2≤y<0,
由方程|2x-1|-|2x+1|=a+1有实数解
∴-2≤a+1<0,
∴-3≤a<-1
故实数a的取值范围[-3,-1).
故答案为:[-3,-1)
B.连接BD,AC,根据弦切角定理∠MAB=∠ACB=∠ADB=25°
∵∠D所对的弧是
 |
| ABC |
∴∠D=∠ADB+∠BDC
∴所求角度为25°+90°=115°
故答案为:115°
C.∵曲线C的参数方程是:
|
∴(x-2)2+(y+1)2=9,
∴圆心0为(2,-1),半径r=3,
直线l的参数方程为
|
∵曲线C被直线l所截,
∴圆心到直线的距离为:d=
| |2+2+1| | ||
|
| 5 |
∴弦长=2×
32-(
|
故答案为:4.
点评:A.方程f(x)=a有实数解,即a属于函数y=f(x)的值域,然后将方程有实根的问题,转化为求函数值域的问题.
B.本题考查同弧所对的圆周角和弦切角相等,考查直径所对的圆周角等于直角,本题只要观察清楚图象中各个角之间的关系,就可以求出角的大小,这种题目隐含的条件比较多,注意挖掘.
C.此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,还考查了直线与圆相交的性质.
B.本题考查同弧所对的圆周角和弦切角相等,考查直径所对的圆周角等于直角,本题只要观察清楚图象中各个角之间的关系,就可以求出角的大小,这种题目隐含的条件比较多,注意挖掘.
C.此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,还考查了直线与圆相交的性质.

练习册系列答案
相关题目
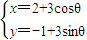 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为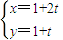 (t为参数),则直线l被曲线C截得的弦长为 .
(t为参数),则直线l被曲线C截得的弦长为 .