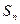摘要：18．已知数列{}.{}, .分别表示{}.{}的前K项和(KN).若+=K.又有=+.求数列{}的通项,欲使大于2004.正整数n至少取何值?
网址：http://m.1010jiajiao.com/timu3_id_4462842[举报]
(本小题满分12分)
已知数列{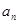
}为公差不为零的等差数列，
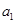=1，各项均为正数的等比数列{
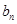}的第1
项、第3项、第5项分别是、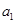
、
．
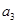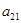(I
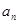)求数列{}与{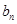}的通项公式；
(Ⅱ)求数列{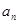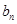}的前
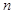项和．
已知数列{
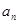}为公差不为零的等差数列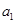，=1，各项均为正数的等比数列{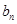}的第1 项、第3项、第5项分别是
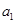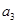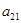、、．(I
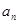)求数列{}与{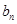}的通项公式；(Ⅱ)求数列{
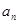
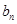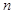}的前项和． (本小题满分12分)
已知等差数列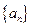
的首项
公差
且第二项、第五项、第十四项分别是等比数列
的第二项、第三项、第四项。
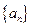（1）求数列与数列的通项公式；
（2）设数列
对任意正整数
均有
成立，
（3）求数列的前项和
(本小题满分12分)已知抛物线方程为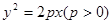
（1）若点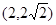
在抛物线上，求抛物线的焦点
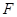的坐标和准线
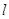的方程；
（2）在（1）的条件下，若过焦点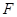且倾斜角为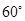
的直线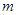
交抛物线于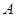
、
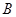两点，点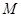
在抛物线的准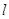线上，直线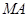
、
、
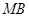的斜率分别记为
、
、
，
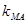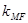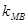求证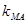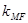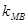：、、成等差数列；
查看习题详情和答案>>
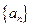的首项
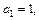公差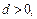
且第二项、第五项、第十四项分别是等比数列
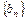的第二项、第三项、第四项。
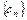对任意正整数
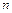均有
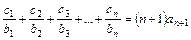成立，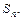
、
、
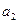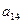分别是一个等比数列的第二项、第三项、第四项．
＝
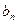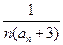（n∈N*），
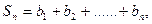求