题目内容
(本小题满分12分)已知抛物线方程为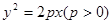
(1)若点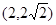 在抛物线上,求抛物线的焦点
在抛物线上,求抛物线的焦点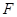 的坐标和准线
的坐标和准线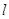 的方程;
的方程;
(2)在(1)的条件下,若过焦点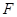 且倾斜角为
且倾斜角为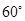 的直线
的直线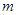 交抛物线于
交抛物线于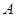 、
、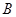 两点,点
两点,点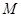 在抛物线的准线
在抛物线的准线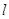 上,直线
上,直线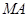 、
、 、
、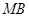 的斜率分别记为
的斜率分别记为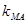 、
、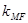 、
、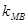 ,
,
求证: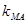 、
、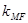 、
、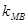 成等差数列;
成等差数列;
【答案】
(1)抛物线的焦点坐标为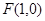 ,准线
,准线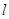 的方程为
的方程为 ;(2)证明:见解析。
;(2)证明:见解析。
【解析】
试题分析:(Ⅰ)根据(2,2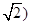 在抛物线y2=2px(p>0)上,可得p=2,从而可求抛物线的焦点坐标与准线l的方程;
在抛物线y2=2px(p>0)上,可得p=2,从而可求抛物线的焦点坐标与准线l的方程;
(Ⅱ)过焦点F(1,0)且倾斜角为60°的直线m的方程为y=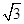 (x-1)与抛物线方程联立,可得点A、B的坐标,设点M的坐标为M(-1,t),即可证得kMA、kMF、kMB成等差数列.
(x-1)与抛物线方程联立,可得点A、B的坐标,设点M的坐标为M(-1,t),即可证得kMA、kMF、kMB成等差数列.
解:(1)
∵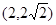 在抛物线上, 由
在抛物线上, 由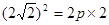 得
得 ……………2分
……………2分
∴抛物线的焦点坐标为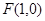 , ……………3分
, ……………3分
准线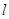 的方程为
的方程为 ……………4分
……………4分
(2)证明:∵抛物线的方程为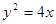 ,
,
∴过焦点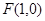 且倾斜角为
且倾斜角为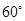 的直线
的直线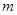 的方程为
的方程为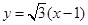 …………5分
…………5分
由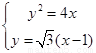 可得
可得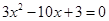
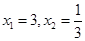
解得点A、B的坐标为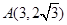 ,
,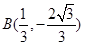 ……………7分
……………7分
∵抛物线的准线方程为 ,设点M的坐标为
,设点M的坐标为 ,……………8分
,……………8分
则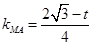 ,
,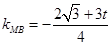 ,
,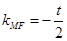 ,…………9分
,…………9分
由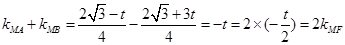 ……………11分
……………11分
知 、
、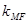 、
、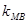 成等差数列。
……………12分
成等差数列。
……………12分
考点:本试题主要考查了直线与圆锥曲线的综合应用能力,涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.
点评:解决该试题的关键是熟练利用抛物线的性质,得到其方程,同时结合设而不求的思想,来表示出点的坐标关系式,结合斜率给弄个是得到证明。

练习册系列答案
相关题目