摘要：14．设数列.其中数列是公差为2的等差数列且 则的值为 .
网址：http://m.1010jiajiao.com/timu3_id_4461685[举报]
设数列{an}的各项都为正数，其前n项和为Sn，已知对任意n∈N*，Sn是an2和an的等差中项．
（Ⅰ）证明数列{an}为等差数列，并求数列{an}的通项公式；
（Ⅱ）证明
+
+…+
＜2；
（Ⅲ）设集合M={m|m=2k，k∈Z，且1000≤k＜1500}，若存在m∈M，使对满足n＞m的一切正整数n，不等式Sn-1005＞
恒成立，求这样的正整数m共有多少个？
查看习题详情和答案>>
（Ⅰ）证明数列{an}为等差数列，并求数列{an}的通项公式；
（Ⅱ）证明
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
（Ⅲ）设集合M={m|m=2k，k∈Z，且1000≤k＜1500}，若存在m∈M，使对满足n＞m的一切正整数n，不等式Sn-1005＞
| ||
| 2 |
设数列{an}（其中n∈N*）是公差不为0的等差数列，Sn为其前n项和，数列{bn}为等比数列且a1=b1=2，S2=5b2，S4=25b3．求数列{an}和数列{bn}的通项公式an及bn．
查看习题详情和答案>>
设数列{an}的前n项和为Sn，其中an≠0，a1为常数，且-a1，Sn，an+1成等差数列．
（1）求{an}的通项公式；
（2）若a1=3，求数列{log3an}的前n项和Rn
（3）设bn=1-Sn，问：是否存在a1，使数列{bn}为等比数列？若存在，求出a1的值；若不存在，请说明理由．
查看习题详情和答案>>
（1）求{an}的通项公式；
（2）若a1=3，求数列{log3an}的前n项和Rn
（3）设bn=1-Sn，问：是否存在a1，使数列{bn}为等比数列？若存在，求出a1的值；若不存在，请说明理由．
在公比为2的等比数列{an}中，a2与a4的等差中项是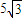
．
（Ⅰ）求a1的值；
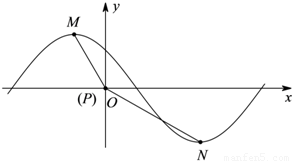
（Ⅱ）若函数y=|a1|sin（
），|ϕ|＜π的一部分图象如图所示，M（-1，|a1|），
为图象上的两点，设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．
查看习题详情和答案>>
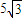．（Ⅰ）求a1的值；
（Ⅱ）若函数y=|a1|sin（
），|ϕ|＜π的一部分图象如图所示，M（-1，|a1|），为图象上的两点，设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．
查看习题详情和答案>>
已知
是公差为d的等差数列，
是公比为q的等比数列
（Ⅰ）若 
，是否存在
，有
？请说明理由；
（Ⅱ）若
（a、q为常数，且aq
0）对任意m存在k，有
，试求a、q满足的充要条件；
（Ⅲ）若
试确定所有的p,使数列中存在某个连续p项的和式数列中的一项，请证明.
【解析】第一问中，由
得
，整理后，可得
、
，
为整数
不存在
、
，使等式成立。
（2）中当
时，则
即
，其中
是大于等于
的整数
反之当时，其中是大于等于的整数，则
，
显然
，其中
、
满足的充要条件是，其中是大于等于的整数
（3）中设
当
为偶数时，
式左边为偶数，右边为奇数，
当为偶数时，式不成立。由式得
，整理
当
时，符合题意。当
，为奇数时，
结合二项式定理得到结论。
解（1）由得，整理后，可得、，为整数不存在、，使等式成立。
（2）当时，则即，其中是大于等于的整数反之当时，其中是大于等于的整数，则，
显然，其中
、满足的充要条件是，其中是大于等于的整数
（3）设当为偶数时，式左边为偶数，右边为奇数，
当为偶数时，式不成立。由式得，整理
当时，符合题意。当，为奇数时，
由，得
当为奇数时，此时，一定有
和
使上式一定成立。当为奇数时，命题都成立
查看习题详情和答案>>