摘要:(三).解答题: 11.求下面各函数中自变量取值范围 (1) (2) (3) 12.的两角的角平分线交于点D.设度数为y.度数 为x.求y关于x的函数解析式及自变量x的取值范围. 13.已知点M坐标为.点N在第三象限坐标为(x,y)且x+y=-6.设 面积为S. (1)求S关于x的函数表达式 (2)求x的取值范围 (3)当S=10时.求N点坐标
网址:http://m.1010jiajiao.com/timu3_id_446123[举报]
注意:为了使学生更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求,进行解答.
如图①,在一幅矩形地毯的四周镶有宽度相同的花边. 如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米,求花边的宽.
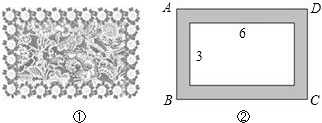
(Ⅰ)设花边的宽为x米,用含x的代数式表示:
矩形地毯ABCD的长为 米;
矩形地毯ABCD的宽为 米;
矩形地毯ABCD的面积为 米2;
(Ⅱ)列出方程,并求出问题的解. 查看习题详情和答案>>
如图①,在一幅矩形地毯的四周镶有宽度相同的花边. 如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米,求花边的宽.

(Ⅰ)设花边的宽为x米,用含x的代数式表示:
矩形地毯ABCD的长为
矩形地毯ABCD的宽为
矩形地毯ABCD的面积为
(Ⅱ)列出方程,并求出问题的解. 查看习题详情和答案>>
(2013•西青区二模)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.
有一工程需在规定日期内完成,如果甲单独工作刚好能够按期完成;如果乙单独工作就要超过规定日期3天.现在甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成,求规定日期是几天?
解题方案:
设规定的日期为x天,
(Ⅰ)用含x的代数式表示:
①甲的工作效率为
;
②乙的工作效率为
;
(Ⅱ)根据题意,列出相应方程
(Ⅲ)解这个方程,得
(Ⅳ)检验:
(Ⅴ)答:规定日期是
查看习题详情和答案>>
有一工程需在规定日期内完成,如果甲单独工作刚好能够按期完成;如果乙单独工作就要超过规定日期3天.现在甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成,求规定日期是几天?
解题方案:
设规定的日期为x天,
(Ⅰ)用含x的代数式表示:
①甲的工作效率为
| 1 |
| x |
| 1 |
| x |
②乙的工作效率为
| 1 |
| x+3 |
| 1 |
| x+3 |
(Ⅱ)根据题意,列出相应方程
(
+
)×2+
×(x-2)=1
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
(
+
)×2+
×(x-2)=1
;| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
(Ⅲ)解这个方程,得
x=6
x=6
;(Ⅳ)检验:
x=6是原方程的根
x=6是原方程的根
;(Ⅴ)答:规定日期是
6天
6天
.
阅读下面计算
+
+
+…+
的过程,然后填空.
解:因为
=
(
-
),
=
(
-
)…
=
(
-
)
所以
+
+
+…+
=
(
-
)+
(
-
)+
(
-
)…+
(
-
)
=
(
-
+
-
+
-
…+
-
)=
(
-
)=
以上方法为裂项求和法,请类比完成:
(1)
+
+
+…+
= .
(2)在和式
+
+
+…+( )=
中最未一项为 .
(3)已知-3x2ya+1+x3y-3x4-2是五次四项式,单项式-3x3by3-a与多项式的次数相同,求
+
+
+
+
+
+
+
-
的值.
查看习题详情和答案>>
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 9×11 |
解:因为
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 9×11 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 11 |
所以
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 9×11 |
=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 11 |
=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 11 |
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 11 |
| 5 |
| 11 |
以上方法为裂项求和法,请类比完成:
(1)
| 1 |
| 2×4 |
| 1 |
| 4×6 |
| 1 |
| 6×8 |
| 1 |
| 18×20 |
(2)在和式
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 6 |
| 13 |
(3)已知-3x2ya+1+x3y-3x4-2是五次四项式,单项式-3x3by3-a与多项式的次数相同,求
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 1 |
| 6×7 |
| 1 |
| 7×8 |
| 1 |
| 8×9 |
| 2 |
| b |
(2013•和平区二模)注意:为了使同学们更好的解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,并完成本题解答的全过程,也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求,进行解答即可.
小丽乘汽车从青岛到黄岛奶奶家,她去时经过环湾高速公路,全程约84千米,返回时经过跨海大桥,全程约45千米,小丽所乘汽车去时的平均速度是返回时的1.2倍,所用时间却比返回时多20分钟,求小丽所乘汽车返回时的平均速度.
(Ⅰ)设小丽所乘汽车返回时的平均速度为x千米/时,利用速度、时间、路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)
(Ⅱ)列出方程(组),并求出问题的解.
查看习题详情和答案>>
小丽乘汽车从青岛到黄岛奶奶家,她去时经过环湾高速公路,全程约84千米,返回时经过跨海大桥,全程约45千米,小丽所乘汽车去时的平均速度是返回时的1.2倍,所用时间却比返回时多20分钟,求小丽所乘汽车返回时的平均速度.
(Ⅰ)设小丽所乘汽车返回时的平均速度为x千米/时,利用速度、时间、路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)
| 速度(千米/时 | 所用时间(时) | 所走的路程(千米) | |||||
| 去时 | 1.2x 1.2x |
|
84 | ||||
| 返回时 | x |
|
45 |
23、注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.青山村种的水稻2007年平均每公顷产8 000kg,2009年平均每公顷产9 680kg,求该村水稻每公顷产量的年平均增长率.
解题方案:
设该村水稻每公顷产量的年平均增长率为x.
(Ⅰ)用含x的代数式表示:
①2008年种的水稻平均每公顷的产量为
②2009年种的水稻平均每公顷的产量为
(Ⅱ)根据题意,列出相应方程
(Ⅲ)解这个方程,得
(Ⅳ)检验:
(Ⅴ)答:该村水稻每公顷产量的年平均增长率为
查看习题详情和答案>>
解题方案:
设该村水稻每公顷产量的年平均增长率为x.
(Ⅰ)用含x的代数式表示:
①2008年种的水稻平均每公顷的产量为
8000(1+x)
;②2009年种的水稻平均每公顷的产量为
8000(1+x)2
;(Ⅱ)根据题意,列出相应方程
8000(1+x)2=9680
;(Ⅲ)解这个方程,得
x1=0.1,x2=-2.1
;(Ⅳ)检验:
x1=0.1,x2=-2.1都是原方程的根,但x2=-2.1不符合题意,所以只取x=0.1
;(Ⅴ)答:该村水稻每公顷产量的年平均增长率为
10
%.