题目内容
（2012•奉贤区一模）出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的．在出租车几何学中，点还是形如（x，y）的有序实数对，直线还是满足ax+by+c=0的所有（x，y）组成的图形，角度大小的定义也和原来一样．直角坐标系内任意两点A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：|AB|=|x1-x2|+|y1-y2|，请解决以下问题：（1）求线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”；
（2）定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”方程；
（3）点A（1，3）、B（6，9），写出线段AB的垂直平分线的轨迹方程并画出大致图象．（说明所给图形小正方形的单位是1）
分析：（1）利用“距离”的定义能够求出线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”．
（2 ）利用“圆”的概念，能够求出“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”的方程．
（3）由已知条件，得|x-1|+|y-3|=|x-6|+|y-9，由此能够求出线段AB的垂直平分线的轨迹方程并画出大致图象．
（2 ）利用“圆”的概念，能够求出“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”的方程．
（3）由已知条件，得|x-1|+|y-3|=|x-6|+|y-9，由此能够求出线段AB的垂直平分线的轨迹方程并画出大致图象．
解答：解：（1）∵任意两点A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：|AB|=|x1-x2|+|y1-y2|，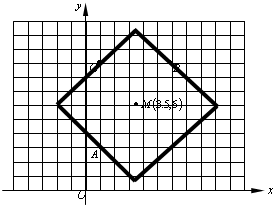
∴线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”：
MO=|x-0|+|y-0|=|x|+|y|=x+y=2．…（3分）
（2 ）∵“圆”是所有到定点“距离”为定值的点组成的图形，
∴“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”方程为：
|x-a|+|y-b|=r…（6分）
（3）由已知条件得|x-1|+|y-3|=|x-6|+|y-9|…（8分）
若x≤1，则y=8.5 …（10分）
若1≤x≤6，则x+y=9.5 …（12分）
若6≤x，则y=3.5 …（14分）
图象如右图所示．…（16分）
∴线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”：
MO=|x-0|+|y-0|=|x|+|y|=x+y=2．…（3分）
（2 ）∵“圆”是所有到定点“距离”为定值的点组成的图形，
∴“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”方程为：
|x-a|+|y-b|=r…（6分）
（3）由已知条件得|x-1|+|y-3|=|x-6|+|y-9|…（8分）
若x≤1，则y=8.5 …（10分）
若1≤x≤6，则x+y=9.5 …（12分）
若6≤x，则y=3.5 …（14分）
图象如右图所示．…（16分）
点评：本题考查“距离”的定义，“圆”的概念，写出线段AB的垂直平分线的轨迹方程并画出大致图象．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目