题目内容
(2012•奉贤区一模)出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的.在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:|AB|=|x1-x2|+|y1-y2|,请解决以下问题:
(1)求点A(1,3)、B(6,9)的“距离”|AB|;
(2)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(3)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点A(1,3)、B(6,9),C(1,9),求经过这三个点确定的一个“圆”的方程,并画出大致图象;(说明所给图形小正方形的单位是1)

(1)求点A(1,3)、B(6,9)的“距离”|AB|;
(2)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(3)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点A(1,3)、B(6,9),C(1,9),求经过这三个点确定的一个“圆”的方程,并画出大致图象;(说明所给图形小正方形的单位是1)

分析:(1)根据出租车几何学中“距离”的定义,易得|AB|=|6-1|+|9-3|=5+6=11;
(2)用出租车几何学中“距离”的定义代入,再结合已知条件去绝对值化简,可得M到原点O的“距离”等于2;
(3)设“圆”的“圆心”坐标为M(m,n),由|MA|=|MB|=|MC|结合绝对值的性质,得到M(
,6),再根据出租车几何学中“距离”的定义,求出“半径”R的值,即可画出这个“圆”的大致图象.
(2)用出租车几何学中“距离”的定义代入,再结合已知条件去绝对值化简,可得M到原点O的“距离”等于2;
(3)设“圆”的“圆心”坐标为M(m,n),由|MA|=|MB|=|MC|结合绝对值的性质,得到M(
| 7 |
| 2 |
解答:解:(1)根据出租车几何学中“距离”的定义,得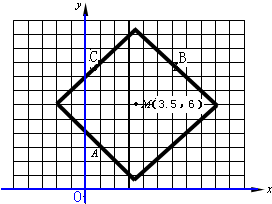
|AB|=|x1-x2|+|y1-y2|=|6-1|+|9-3|=5+6=11…(3分)
(2)点M(x,y)到原点的距离为:|MO|=|x-0|+|y-0|=|x|+|y|
∵线段x+y=2上的点M(x,y)满足x≥0,y≥0
∴|x|=x,|y|=y=2-x,可得|MO|=|x|+|y|=x+y=2…(6分)
(3)设“圆心”坐标为M(m,n),则
由|MA|=|MC|,得|m-1|+|n-3|=|m-1|+|n-9|,所以点M在y=6上…(7分)
又因为|MB|=|MC|即|m-1|+|n-9|=|m-6|+|n-9|,所以点M在x=
上…(8分)
∴M(
,6)…(10分)
R=|AM|=|
-1|+|6-3|=
…(14分)
“圆M”的图象如右图所示 …(16分)

|AB|=|x1-x2|+|y1-y2|=|6-1|+|9-3|=5+6=11…(3分)
(2)点M(x,y)到原点的距离为:|MO|=|x-0|+|y-0|=|x|+|y|
∵线段x+y=2上的点M(x,y)满足x≥0,y≥0
∴|x|=x,|y|=y=2-x,可得|MO|=|x|+|y|=x+y=2…(6分)
(3)设“圆心”坐标为M(m,n),则
由|MA|=|MC|,得|m-1|+|n-3|=|m-1|+|n-9|,所以点M在y=6上…(7分)
又因为|MB|=|MC|即|m-1|+|n-9|=|m-6|+|n-9|,所以点M在x=
| 7 |
| 2 |
∴M(
| 7 |
| 2 |
R=|AM|=|
| 7 |
| 2 |
| 11 |
| 2 |
“圆M”的图象如右图所示 …(16分)
点评:本题给出一个新的定义,叫我们求该定义下的“距离”和“圆”的图象,着重考查了对新定义的理解和进行简单的演绎推理等知识,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目