摘要：9．设定义在实数集上的函数f(x)对任意x∈R均有f(x)+f(2-x)=1.则这个函数的图象必关于 ( ) A．直线x=1对称 B．点(1.1)对称 C．点(1.)对称 D．点(2.1)对称
网址：http://m.1010jiajiao.com/timu3_id_4458901[举报]
设定义在实数集上的函数f(x)对任意x∈R均有f(x)+f(2－x)=1，则这个函数的图象必关于（ ）
A．直线x=1对称 B．点（1，1）对称
C．点（1，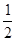
）对称 D．点（2，1）对称
查看习题详情和答案>>
设定义在实数集上的函数f(x)对任意x∈R均有f(x)+f(2－x)=1，则这个函数的图象必关于（ ）
| A．直线x=1对称 | B．点（1，1）对称 |
C．点（1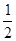， ）对称 | D．点（2，1）对称 |
若定义在区间D上的函数y=f（x）对于区间D上的任意两个值x1、x2总有以下不等式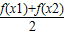
≤f（
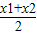）成立，则称函数y=f（x）为区间D上的凸函数．
（1）证明：定义在R上的二次函数f（x）=ax2+bx+c（a＜0）是凸函数；
（2）设f（x）=ax2+x（a∈R，a≠0），并且x∈[0，1]时，f（x）≤1恒成立，求实数a的取值范围，并判断函数
f（x）=ax2+x（a∈R，a≠0）能否成为R上的凸函数；
（3）定义在整数集Z上的函数f（x）满足：①对任意的x，y∈Z，f（x+y）=f（x）f（y）；②f（0）≠0，f（1）=2．
试求f（x）的解析式；并判断所求的函数f（x）是不是R上的凸函数说明理由．
查看习题详情和答案>>
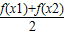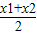≤f（）成立，则称函数y=f（x）为区间D上的凸函数．（1）证明：定义在R上的二次函数f（x）=ax2+bx+c（a＜0）是凸函数；
（2）设f（x）=ax2+x（a∈R，a≠0），并且x∈[0，1]时，f（x）≤1恒成立，求实数a的取值范围，并判断函数
f（x）=ax2+x（a∈R，a≠0）能否成为R上的凸函数；
（3）定义在整数集Z上的函数f（x）满足：①对任意的x，y∈Z，f（x+y）=f（x）f（y）；②f（0）≠0，f（1）=2．
试求f（x）的解析式；并判断所求的函数f（x）是不是R上的凸函数说明理由．
查看习题详情和答案>>
| |||||
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
时，
，则有
