摘要：21．在三棱锥S-ABC中.△ABC是边长为4的正三角形.面SAC⊥ABC.SA=SC=.M.N分别为AB.SB的中点. (1)证明AC⊥SB, (2)求二面角N-CM-B的正切值大小, (3)求点B到面CMN的距离. 2,4,6
网址：http://m.1010jiajiao.com/timu3_id_4457213[举报]
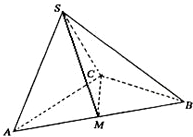在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2| 2 |
（Ⅰ）证明：AC⊥SB；
（Ⅱ）求二面角S-CM-B的大小；
（Ⅲ）求点B到平面SCM的距离． 查看习题详情和答案>>
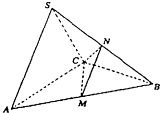在三棱锥S-ABC中，△ABC是边长为4的正三角形，点S在平面ABC上的射影恰为AC的中点，SA=2| 3 |
（1）证明AC丄SB；
（2）求直线CN与平面ABC所成角的余弦值；
（3）求点B到平面CMN的距离． 查看习题详情和答案>>
在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2
，M，N分别为AB，SB的中点．
（1）证明：AC⊥SB；
（2）求二面角N-CM-B的大小；
（3）求点B到平面CMN的距离．
查看习题详情和答案>>
| 3 |
（1）证明：AC⊥SB；
（2）求二面角N-CM-B的大小；
（3）求点B到平面CMN的距离．
在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2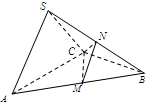
在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，