摘要:22.已知函数上每一点处可导的函数.若在 上恒成立. (1)证明函数在上是单调递增函数, (2)用数学归纳法证明:对于任意的 恒成立, (3)已知不等式时恒成立.求证:
网址:http://m.1010jiajiao.com/timu3_id_4456842[举报]
已知函数f(x)是在(0,+∞)上每一点处可导的函数,若xf′(x)>f(x)在(0,+∞)上恒成立.
(Ⅰ)求证:函数g(x)=
在(0,+∞)上单调递增;
(Ⅱ)当x1>0,x2>0时,证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)已知不等式ln(1+x)<x在x>-1且x≠0时恒成立,证明:
ln22+
ln32+
ln42+…+
ln(n+1)2>
(n∈N+).
查看习题详情和答案>>
(Ⅰ)求证:函数g(x)=
| f(x) |
| x |
(Ⅱ)当x1>0,x2>0时,证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)已知不等式ln(1+x)<x在x>-1且x≠0时恒成立,证明:
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| n |
| 2(n+1)(n+2) |
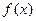 是在
是在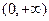 上每一点处均可导的函数,若
上每一点处均可导的函数,若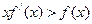 在
在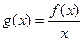 在
在 时,证明:
时,证明: ;
;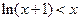 在
在 且
且 时恒成立,求证:
时恒成立,求证: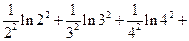 …
…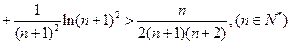
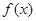 是在
是在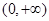 上每一点处均可导的函数,若
上每一点处均可导的函数,若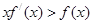 在
在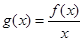 在
在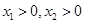 时,证明:
时,证明: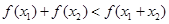 ;
;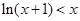 在
在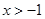 且
且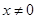 时恒成立,求证:
时恒成立,求证: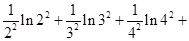 …
…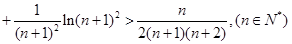
 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;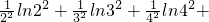 …
…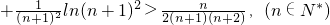 .
.