题目内容
(20分)已知函数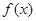 是在
是在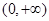 上每一点处均可导的函数,若
上每一点处均可导的函数,若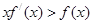 在
在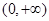 上恒成立。
上恒成立。
(1)①求证:函数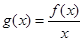 在
在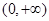 上是增函数;
上是增函数;
②当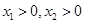 时,证明:
时,证明: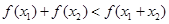 ;
;
(2)已知不等式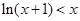 在
在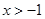 且
且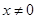 时恒成立,求证:
时恒成立,求证:
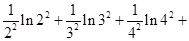 …
…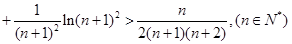
【答案】
解(1)①由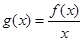 ,
,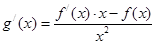 ,由
,由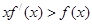 可知
可知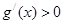 在
在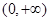 上恒成立,
上恒成立,
从而有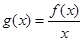 在
在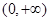 上是增函数。
上是增函数。
②由①知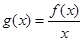 在
在 上是增函数,当
上是增函数,当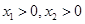 时,有
时,有
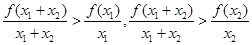 ,于是有:
,于是有:
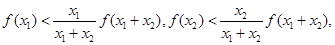 两式相加得:
两式相加得: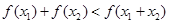
(2)由(Ⅰ)②可知: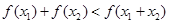 ,(
,(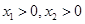 )恒成立
)恒成立
由数学归纳法可知: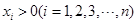 时,有:
时,有:
 恒成立
恒成立
设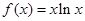 ,则,则
,则,则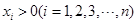 时,
时,
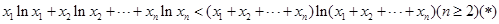 恒成立
恒成立
令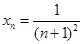 ,记
,记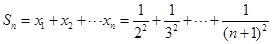
又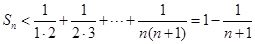 ,
,
又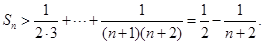
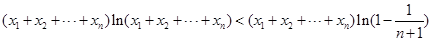
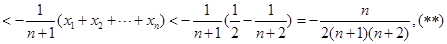
将(**)代入(*)中,可知: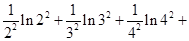 …
…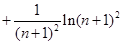
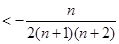
于是: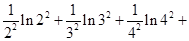 …
…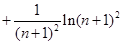
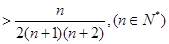
【解析】略

练习册系列答案
相关题目
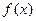 是在
是在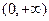 上每一点处均可导的函数,若
上每一点处均可导的函数,若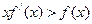 在
在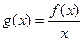 在
在 时,证明:
时,证明: ;
;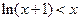 在
在 且
且 时恒成立,求证:
时恒成立,求证: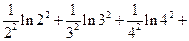 …
…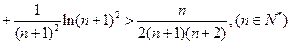
 是在
是在 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在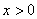 时恒成立.
时恒成立.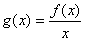 在
在 时,有
时,有 ;
;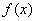 是在
是在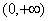 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在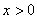 时恒成立.
时恒成立.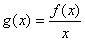 在
在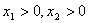 时,有
时,有 ;
;