题目内容
已知函数f(x)是在(0,+∞)上每一点处可导的函数,若xf′(x)>f(x)在(0,+∞)上恒成立.
(Ⅰ)求证:函数g(x)=
在(0,+∞)上单调递增;
(Ⅱ)当x1>0,x2>0时,证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)已知不等式ln(1+x)<x在x>-1且x≠0时恒成立,证明:
ln22+
ln32+
ln42+…+
ln(n+1)2>
(n∈N+).
(Ⅰ)求证:函数g(x)=
| f(x) |
| x |
(Ⅱ)当x1>0,x2>0时,证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)已知不等式ln(1+x)<x在x>-1且x≠0时恒成立,证明:
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| n |
| 2(n+1)(n+2) |
分析:(I)先利用导数的四则运算,求函数g(x)的导函数,结合已知证明导函数g′(x)>0在(0,+∞)上恒成立,即可证明其在(0,+∞)上是增函数;
(Ⅱ)由(Ⅰ)知,x1>0,x2>0时,有
>
,
>
,由此可得结论.
(Ⅲ)由于
ln(n+1)2=-
ln
,故构造一个符合条件的函数f(x)=xlnx,利用(I)的结论,得x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+…+xn)ln(x1+x2+…+xn)(n≥2),令xn=
,记Sn=x1+x2+…xn=
+
+…+
,利用放缩法,即可证明结论.
(Ⅱ)由(Ⅰ)知,x1>0,x2>0时,有
| f(x1+x2) |
| x1+x2 |
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
| f(x2) |
| x2 |
(Ⅲ)由于
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
解答:证明:(Ⅰ)∵g(x)=
,∴g′(x)=
∵xf′(x)>f(x),∴g′(x)>0在(0,+∞)上恒成立,
从而有g(x)=
在(0,+∞)上单调递增;
(Ⅱ)由(Ⅰ)知,x1>0,x2>0时,有
>
,
>
,
于是有:f(x1)<
f(x1+x2),f(x2)<
f(x1+x2),
两式相加得:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)由于
ln(n+1)2=-
ln
,设f(x)=xlnx,则xf′(x)>f(x)在(0,+∞)上恒成立.
由(Ⅱ)可知:f(x1)+f(x2)<f(x1+x2),(x1>0,x2>0)恒成立
由数学归纳法可知:xi>0(i=1,2,3,…,n)时,有:f(x1)+f(x2)+f(x3)+…+f(xn)<f(x1+x2+x3+…xn)(n≥2)恒成立
xi>0(i=1,2,3,…,n)时,x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+…+xn)ln(x1+x2+…+xn)(n≥2)(*)恒成立
令xn=
,记Sn=x1+x2+…xn=
+
+…+
∴Sn<
+
+…+
=1-
,
又Sn>
+…+
=
-
,且ln(x+1)<x
∴(x1+x2+…+xn)ln(x1+x2+…+xn)<(x1+x2+…+xn)ln(1-
)<-
(x1+x2+…+xn)<-
(
-
)=-
(**)
将(**)代入(*)中,可知-[
ln22+
ln32+
ln42+…+
ln(n+1)2]<-
∴
ln22+
ln32+
ln42+…+
ln(n+1)2>
| f(x) |
| x |
| f′(x)•x-f(x) |
| x2 |
∵xf′(x)>f(x),∴g′(x)>0在(0,+∞)上恒成立,
从而有g(x)=
| f(x) |
| x |
(Ⅱ)由(Ⅰ)知,x1>0,x2>0时,有
| f(x1+x2) |
| x1+x2 |
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
| f(x2) |
| x2 |
于是有:f(x1)<
| x1 |
| x1+x2 |
| x2 |
| x1+x2 |
两式相加得:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)由于
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
由(Ⅱ)可知:f(x1)+f(x2)<f(x1+x2),(x1>0,x2>0)恒成立
由数学归纳法可知:xi>0(i=1,2,3,…,n)时,有:f(x1)+f(x2)+f(x3)+…+f(xn)<f(x1+x2+x3+…xn)(n≥2)恒成立
xi>0(i=1,2,3,…,n)时,x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+…+xn)ln(x1+x2+…+xn)(n≥2)(*)恒成立
令xn=
| 1 |
| (n+1)2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
∴Sn<
| 1 |
| 1•2 |
| 1 |
| 2•3 |
| 1 |
| n(n+1) |
| 1 |
| n+1 |
又Sn>
| 1 |
| 2•3 |
| 1 |
| (n+1)(n+2) |
| 1 |
| 2 |
| 1 |
| n+2 |
∴(x1+x2+…+xn)ln(x1+x2+…+xn)<(x1+x2+…+xn)ln(1-
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+1)(n+2) |
将(**)代入(*)中,可知-[
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| n |
| 2(n+1)(n+2) |
∴
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| n |
| 2(n+1)(n+2) |
点评:本题考查了导数的四则运算,考查利用导数证明函数的单调性,利用函数的单调性证明不等式,以及利用函数性质构造数列证明数列不等式的方法,难度较大.

练习册系列答案
相关题目
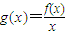 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;