摘要:16.本小题满分13分 解(Ⅰ)①当直线垂直于轴时.则此时直线方程为.与圆的两个交点坐标为和.其距离为 满足题意 1分 ②若直线不垂直于轴.设其方程为.即 2分 设圆心到此直线的距离为.则.得 3分 ∴.. 4分 故所求直线方程为 5分 综上所述.所求直线为或 6分 (Ⅱ)设点的坐标为().点坐标为 则点坐标是 7分 ∵. ∴ 即. 9分 又∵.∴ 11分 ∴点的轨迹方程是. 12分 轨迹是一个焦点在轴上的椭圆.除去短轴端点. 13分 注:多端点时.合计扣1分.
网址:http://m.1010jiajiao.com/timu3_id_4456437[举报]
(本小题满分13分)
已知函数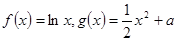 (
(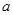 为常数),直线l与函数
为常数),直线l与函数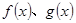 的图象都相切,且l与函数
的图象都相切,且l与函数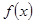 的图象的切点的横坐标为l.
的图象的切点的横坐标为l.
(Ⅰ)求直线l的方程及a的值;
(Ⅱ)当k>0时,试讨论方程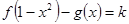 的解的个数.
的解的个数.
查看习题详情和答案>>
(本小题满分13分)
已知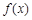 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且 ,若任意的
,若任意的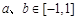 ,当
,当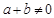 时,总有
时,总有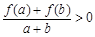 .
.
(1)判断函数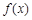 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式: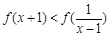 ;
;
(3)若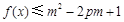 对所有的
对所有的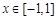 恒成立,其中
恒成立,其中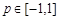 (
(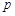 是常数),试用常数
是常数),试用常数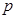 表示实数
表示实数 的取值范围.
的取值范围.
查看习题详情和答案>>
(本小题满分13分)某厂用甲、乙两种产品,已知生产1吨A产品,1吨B产品分别需要的甲乙原料数、可获得的利润及该厂现有原料数如表:
产品 所需原料 | A产品(t) | B产品(t) | 现有原料(t) |
甲(t) | 2 | 1 | 14 |
乙(t) | 1 | 3 | 18 |
利润(万元) | 5 | 3 |
|
(1)在现有原料下,A、B产品应各生产多少才能使利润最大?
(2)如果1吨B产品的利润增加到20万元,原来的最优解为何改变?
(3)如果1吨B产品的利润减少1万元,原来的最优解为何改变?
(4)1吨B产品的利润在什么范围,原最优解才不会改变?
查看习题详情和答案>>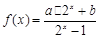 的反函数
的反函数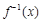 的图象过点
的图象过点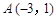 .
.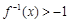 .
.
 时,解不等式
时,解不等式 >
> ;
; 的奇偶性,并说明理由.
的奇偶性,并说明理由.