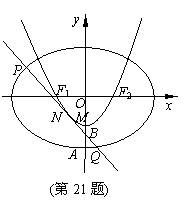
摘要:21. 如图.F1.F2分别是椭圆 (a>b>0)的左右焦点.M为椭圆上一点. MF2垂直于x轴.且OM与椭圆长轴和短轴端点的连线AB平行. (I)求椭圆的离心率, (II)若G为椭圆上不同于长轴端点任一点.求∠F1GF2的取值范围, (Ⅲ)过F2且与OM垂直的直线交椭圆于P.Q两点. 若=20.求椭圆的方程.
网址:http://m.1010jiajiao.com/timu3_id_4456410[举报]
(本小题满分12分)
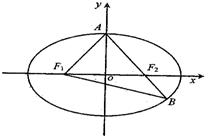
如图,已知椭圆方程![]() ,F1、F2分别为椭圆的左、右焦点,A为椭圆的一顶点,直线AF2交椭圆于点B.
,F1、F2分别为椭圆的左、右焦点,A为椭圆的一顶点,直线AF2交椭圆于点B.
(1)若∠F1AB![]() 90°,求椭圆的离心率;
90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且![]() ,求椭圆的方程.
,求椭圆的方程.
((本小题满分12分)

如图,已知椭圆方程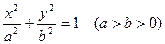 ,
,
F1、F2分别为椭圆的左、右焦点,A为
椭圆的一顶点,直线AF2交椭圆于点B.
(1)若∠F1AB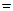 90°,求椭圆的离心率;
90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且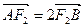 ,
,
求椭圆的方程.

如图,已知椭圆方程
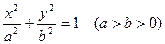 ,
,F1、F2分别为椭圆的左、右焦点,A为
椭圆的一顶点,直线AF2交椭圆于点B.
(1)若∠F1AB
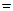 90°,求椭圆的离心率;
90°,求椭圆的离心率;(2)若椭圆的焦距为2,且
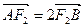 ,
,求椭圆的方程.
 (本小题满分12分) 设椭圆C1:
(本小题满分12分) 设椭圆C1:![]() 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:![]() 与y轴的交点为B,且经过F1,F2点.
与y轴的交点为B,且经过F1,F2点.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设M(0,![]() ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求![]() 面积的最大值.
面积的最大值.
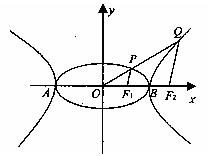
 的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。 的值。
的值。
 的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。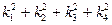 的值。
的值。