Question

（本小题满分12分）

        如图，A、B分别是椭圆的公共左右顶点，P、Q分别位于椭圆和双曲线上且不同于A、B的两点，设直线AP、BP、AQ、BQ的斜率分别为k₁、k₂、k₃、k₄且k₁+k₂­+k₃+k₄=0。

   （1）求证：O、P、Q三点共线；（O为坐标原点）

   （2）设F₁、F₂分别是椭圆和双曲线的右焦点，已知PF₁//QF₂，求的值。

 

 

Answer 1

【答案】

略

【解析】（1）设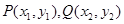，则

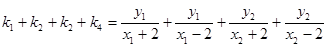
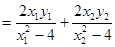   ………………2分

又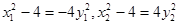

所以

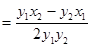…………4分

由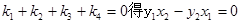

即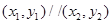

所以O、P、Q三点共线   ………………6分

   （2）

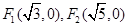
由PF₁//QF₂知|OP|：|OQ|=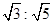

因为O、P、Q三点共线，[来源:ZXXK]

所以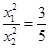  …………①  …………7分

设直线PQ的斜率为k，则

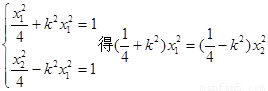  …………②

由①②得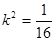   ………………10分

又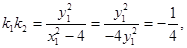

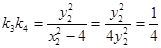   ………………12分

从而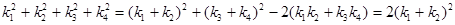

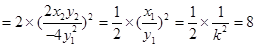  6…………14分