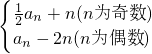摘要：21．已知数列满足: (1)求a2 , a3 , a4 , a5 ; (2)设,求证是等比数列.并求其通项公式, 条件下.求数列前100项中的所有偶数项的和S.

网址：http://m.1010jiajiao.com/timu3_id_4455685[举报]

已知数列{a_n}满足：a₁=1，a_n+1=

an+n(n为奇数)

an-2n(n为偶数)

（1）求a₂，a₃，a₄，a₅；
（2）设b_n=a_2n+1+4n-2，n∈N^*，求证：数列{b_n}是等比数列，并求其通项公式；
（3）求数列{a_n}前100项中的所有奇数项的和S．查看习题详情和答案>>

已知数列{a_n}与{b_n}满足：bnan+an+1+bn+1an+2=0，bn=

，n∈N^*，且a₁=2，a₂=4．
（Ⅰ）求a₃，a₄，a₅的值；
（Ⅱ）设c_n=a_2n-1+a_2n+1，n∈N^*，证明：{c_n}是等比数列；
（Ⅲ）设S_k=a₂+a₄+…+a_2k，k∈N^*，证明：

(n∈N*)．查看习题详情和答案>>

已知数列{a_n}满足：a1=-1，an+1=(1+cos2

，n∈N*．
（1）求a₂，a₃，a₄；并证明：a_2m+1+2=2（a_2m-1+2），m∈N^*（2）设fn(x)=

+rcos[(a1+2)x]+r2cos[(a3+2)x]+r3cos[(a5+2)x]+…+rn-1cos[(a2n-3+2)x]（n≥2，n∈N^*）
①证明：对任意x∈R，当|r|≤

时，rcos[(a1+2)x]+r2cos[(a3+2)x]≥-

②证明：当|r|≤

，f_2n+1（x）对任意x∈R和自然数n（n≥2）都有f_2n+1（x）＞0．

查看习题详情和答案>>

已知数列{a_n}满足：a₁=1，a_n+1=

an+n，n为奇数

an-2n，n为偶数

（1）求a₂、a₃、a₄、a₅；
（2）设b_n=a_2n-2，n∈N，求证{b_n}是等比数列，并求其通项公式；
（3）在（2）条件下，求证数列{a_n}前100项中的所有偶数项的和S₁₀₀＜100．查看习题详情和答案>>

已知数列{a_n}满足：a₁=1，a_n+1= $数学公式$
（1）求a₂，a₃，a₄，a₅；
（2）设b_n=a_2n+1+4n-2，n∈N^*，求证：数列{b_n}是等比数列，并求其通项公式；
（3）求数列{a_n}前100项中的所有奇数项的和S．

查看习题详情和答案>>