摘要：18．已知抛物线经过坐标原点O． (1)求这条抛物线的顶点P的坐标, (2)设这条抛物线与x轴的另一个交点为A.求以直线PA为图象的一次函数解析式．
网址：http://m.1010jiajiao.com/timu3_id_445567[举报]
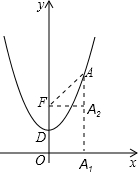
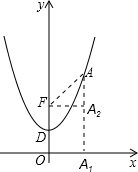
已知抛物线顶点D （0，
），且经过点A（1，
）．
（1）求这条抛物线的解析式；
（2）点F是坐标原点O关于该抛物线顶点的对称点，坐标为（0，
）．我们可以用以下方法求线段FA的长度；过点A作AA1⊥x轴，过点F作x轴的平行线，交AA1于A2，则FA2=1，A2A=
-
=
，在Rt△AFA2中，有FA=
=
．已知抛物线上另一点B的横坐标为2，求线段FB的长；
（3）若点P是该抛物线在第一象限上的任意一点，试探究线段FP的长度与点P纵坐标的大小关系，并证明你的猜想．
查看习题详情和答案>>
| 1 |
| 8 |
| 17 |
| 8 |
（1）求这条抛物线的解析式；
（2）点F是坐标原点O关于该抛物线顶点的对称点，坐标为（0，
| 1 |
| 4 |
| 17 |
| 8 |
| 1 |
| 4 |
| 15 |
| 8 |
12+(
|
| 17 |
| 8 |
（3）若点P是该抛物线在第一象限上的任意一点，试探究线段FP的长度与点P纵坐标的大小关系，并证明你的猜想．
查看习题详情和答案>>
已知抛物线y=ax2+bx+c经过A（-4，3）、B（2，0）两点，当x=3和x=-3时，这条抛物线上对应点的纵坐标相等．经过点C（0，-2）的直线l与x轴平行，O为坐标原点．（1）求直线AB和这条抛物线的解析式；
（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；
（3）设直线AB上的点D的横坐标为-1，P（m，n）是抛物线y=ax2+bx+c上的动点，当△PDO的周长最小时，求四边形CODP的面积． 查看习题详情和答案>>
已知抛物线y=x2+bx+c经过原点，且在x轴的正半轴上截得的线段长为4，对称轴为直线x=m．过点A的直线绕点A （ m，0 ） 旋转，交抛物线于点B （ x，y ），交y轴负半轴于点C，过点C且平行于x轴的直线与直线x=m交于点D，设△AOB的面积为S1，△ABD的面积为S2．
（1）求这条抛物线的顶点的坐标；
（2）判断S1与S2的大小关系，并证明你的结论． 查看习题详情和答案>>
（1）求这条抛物线的顶点的坐标；
（2）判断S1与S2的大小关系，并证明你的结论． 查看习题详情和答案>>
），且经过点A（1，
）．
）．我们可以用以下方法求线段FA的长度；过点A作AA1⊥x轴，过点F作x轴的平行线，交AA1于A2，则FA2=1，A2A=
，在Rt△AFA2中，有FA=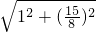
=
