题目内容
 已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与x轴平行,O为坐标原点.
已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与x轴平行,O为坐标原点.(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
分析:(1)用待定系数法即可求出直线AB的解析式;根据“当x=3和x=-3时,这条抛物线上对应点的纵坐标相等”可知:抛物线的对称轴为y轴,然后用待定系数法即可求出抛物线的解析式;
(2)根据A点坐标可求出半径OA的长,然后判断A到直线l的距离与半径OA的大小关系即可;
(3)根据直线AB的解析式可求出D点的坐标,即可得到OD的长,由于OD的长为定值,若△POD的周长最小,那么PD+OP的长最小,可过P作y轴的平行线,交直线l于M;首先证PO=PM,此时PD+OP=PD+PM,而PD+PM≥DM,因此PD+PM最小时,应有PD+PM=DM,即D、P、M三点共线,由此可求得P点的坐标;此时四边形CODP是梯形,根据C、O、D、P四点坐标即可求得上下底DP、OC的长,而梯形的高为D点横坐标的绝对值由此可求出四边形CODP的面积.
(2)根据A点坐标可求出半径OA的长,然后判断A到直线l的距离与半径OA的大小关系即可;
(3)根据直线AB的解析式可求出D点的坐标,即可得到OD的长,由于OD的长为定值,若△POD的周长最小,那么PD+OP的长最小,可过P作y轴的平行线,交直线l于M;首先证PO=PM,此时PD+OP=PD+PM,而PD+PM≥DM,因此PD+PM最小时,应有PD+PM=DM,即D、P、M三点共线,由此可求得P点的坐标;此时四边形CODP是梯形,根据C、O、D、P四点坐标即可求得上下底DP、OC的长,而梯形的高为D点横坐标的绝对值由此可求出四边形CODP的面积.
解答:解:(1)设直线AB的解析式为y=kx+b,则有:
,
解得
;
∴直线AB的解析式为y=-
x+1;
由题意知:抛物线的对称轴为y轴,则抛物线经过(-4,3),(2,0),(-2,0)三点;
设抛物线的解析式为:y=a(x-2)(x+2),
则有:3=a(-4-2)(-4+2),a=
;
∴抛物线的解析式为:y=
x2-1;
(2)易知:A(-4,3),则OA=
=5;
而A到直线l的距离为:3-(-2)=5;
所以⊙A的半径等于圆心A到直线l的距离,
即直线l与⊙A相切;
(3)过D点作DM∥y轴交直线于点M交抛物线于点P,
则P(m,n),M(m,-2);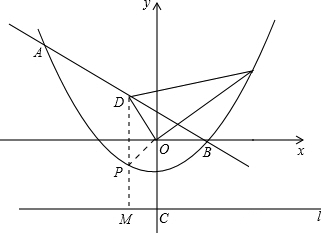
∴PO2=m2+n2,PM2=(n+2)2;
∵n=
m2-1,即m2=4n+4;
∴PO2=n2+4n+4=(n+2)2,
即PO2=PM2,PO=PM;
易知D(-1,
),则OD的长为定值;
若△PDO的周长最小,则PO+PD的值最小;
∵PO+PD=PD+PM≥DM,
∴PD+PO的最小值为DM,
即当D、P、M三点共线时PD+PM=PO+PD=DM;
此时点P的横坐标为-1,代入抛物线的解析式可得y=
-1=-
,
即P(-1,-
);
∴S四边形CPDO=
(CO+PD)×|xD|=
×(2+
+
)×1=
.
|
解得
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
由题意知:抛物线的对称轴为y轴,则抛物线经过(-4,3),(2,0),(-2,0)三点;
设抛物线的解析式为:y=a(x-2)(x+2),
则有:3=a(-4-2)(-4+2),a=
| 1 |
| 4 |
∴抛物线的解析式为:y=
| 1 |
| 4 |
(2)易知:A(-4,3),则OA=
| 42+32 |
而A到直线l的距离为:3-(-2)=5;
所以⊙A的半径等于圆心A到直线l的距离,
即直线l与⊙A相切;
(3)过D点作DM∥y轴交直线于点M交抛物线于点P,
则P(m,n),M(m,-2);

∴PO2=m2+n2,PM2=(n+2)2;
∵n=
| 1 |
| 4 |
∴PO2=n2+4n+4=(n+2)2,
即PO2=PM2,PO=PM;
易知D(-1,
| 3 |
| 2 |
若△PDO的周长最小,则PO+PD的值最小;
∵PO+PD=PD+PM≥DM,
∴PD+PO的最小值为DM,
即当D、P、M三点共线时PD+PM=PO+PD=DM;
此时点P的横坐标为-1,代入抛物线的解析式可得y=
| 1 |
| 4 |
| 3 |
| 4 |
即P(-1,-
| 3 |
| 4 |
∴S四边形CPDO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 17 |
| 8 |
点评:此题主要考查了二次函数解析式的确定、直线与圆的位置关系、图形面积的求法等知识,还涉及到解析几何中抛物线的相关知识,能力要求极高,难度很大.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=