题目内容
已知抛物线顶点D (0, ),且经过点A(1,
),且经过点A(1, ).
).
(1)求这条抛物线的解析式;
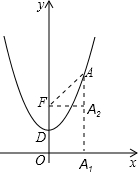
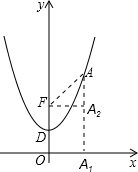
(2)点F是坐标原点O关于该抛物线顶点的对称点,坐标为(0, ).我们可以用以下方法求线段FA的长度;过点A作AA1⊥x轴,过点F作x轴的平行线,交AA1于A2,则FA2=1,A2A=
).我们可以用以下方法求线段FA的长度;过点A作AA1⊥x轴,过点F作x轴的平行线,交AA1于A2,则FA2=1,A2A= -
- =
= ,在Rt△AFA2中,有FA=
,在Rt△AFA2中,有FA=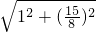 =
= .已知抛物线上另一点B的横坐标为2,求线段FB的长;
.已知抛物线上另一点B的横坐标为2,求线段FB的长;
(3)若点P是该抛物线在第一象限上的任意一点,试探究线段FP的长度与点P纵坐标的大小关系,并证明你的猜想.
解:(1)设抛物线顶点式:y=a(x-h)2+k,
∵抛物线顶点D (0, ),且经过点A(1,
),且经过点A(1, ).
).
∴a(1-0)2+ =
= ,
,
解得a=2,
∴这条抛物线的解析式为y=2x2+ ;
;
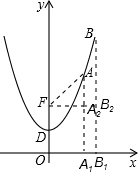
(2)∵点B的横坐标为2,∴点B的纵坐标为 ,
,
过点B作BB1⊥x轴,过点F作x轴的平行线,交BB1于B2,
∴FB2=2,B2B= -
- =
=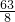 ,
,
在Rt△BFB2中,∴FB=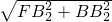 =
=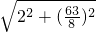 =
= .
.
(3)相等,理由如下:
设点P的坐标为(a,2a2+ ),
),
过点P作PP1⊥x轴,过点F作x轴的平行线,交PP1于P2,
∴FP2=a,P2P=2a2+ -
- =2a2-
=2a2- ,
,
在Rt△PFP2中,∴FP=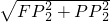 =
=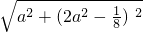 =
=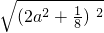 =2a2+
=2a2+ .
.
∴线段FP的长度与点P纵坐标相等.
分析:(1)根据题意设抛物线顶点式:y=a(x-h)2+k,再将AD两点代入即可得出这条抛物线的解析式;
(2)先将点B的横坐标代入抛物线解析式,求出纵坐标,过点B作BB1⊥x轴,过点F作x轴的平行线,交BB1于B2,求得FB2=2,B2B,在Rt△BFB2中,由勾股定理求出FB=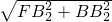 .
.
(3)
点评:本题是一道综合性的题目,考查了用待定系数法求二次函数的解析式,勾股定理二次函数的顶点式等知识点的综合运用,难度较大.
∵抛物线顶点D (0,
 ),且经过点A(1,
),且经过点A(1, ).
).∴a(1-0)2+
 =
= ,
,解得a=2,
∴这条抛物线的解析式为y=2x2+
 ;
;
(2)∵点B的横坐标为2,∴点B的纵坐标为
 ,
,过点B作BB1⊥x轴,过点F作x轴的平行线,交BB1于B2,
∴FB2=2,B2B=
 -
- =
=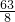 ,
,在Rt△BFB2中,∴FB=
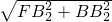 =
=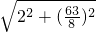 =
= .
.(3)相等,理由如下:

设点P的坐标为(a,2a2+
 ),
),过点P作PP1⊥x轴,过点F作x轴的平行线,交PP1于P2,
∴FP2=a,P2P=2a2+
 -
- =2a2-
=2a2- ,
,在Rt△PFP2中,∴FP=
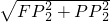 =
=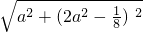 =
=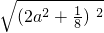 =2a2+
=2a2+ .
.∴线段FP的长度与点P纵坐标相等.
分析:(1)根据题意设抛物线顶点式:y=a(x-h)2+k,再将AD两点代入即可得出这条抛物线的解析式;
(2)先将点B的横坐标代入抛物线解析式,求出纵坐标,过点B作BB1⊥x轴,过点F作x轴的平行线,交BB1于B2,求得FB2=2,B2B,在Rt△BFB2中,由勾股定理求出FB=
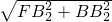 .
.(3)
点评:本题是一道综合性的题目,考查了用待定系数法求二次函数的解析式,勾股定理二次函数的顶点式等知识点的综合运用,难度较大.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.