摘要:在数列中...且当时.. (1)求证数列为等差数列, (2)求数列的通项, (3)当时.设.求证:.
网址:http://m.1010jiajiao.com/timu3_id_4455485[举报]
在数列{an}中,a1=0,a2=2,且当n≥2时,数列{an}的前n项和Sn满足Sn=
.
(I)求数列{an}通项公式;
(Ⅱ)令Pn=
+
,Qn是数列{Pn}的前n项和,求证:Qn<2n+3.
查看习题详情和答案>>
| nan |
| 2 |
(I)求数列{an}通项公式;
(Ⅱ)令Pn=
| Sn+2 |
| Sn+1 |
| Sn+1 |
| Sn+2 |
数列{an},{bn}(n=1,2,3,…)由下列条件确定:①a1<0,b1>0;②当k≥2时,ak与bk满足:ak-1+bk-1≥0时,ak=ak-1,bk=
;当ak-1+bk-1<0时,ak=
,bk=bk-1.
(Ⅰ)若a1=-1,b1=1,,求a2,a3,a4,并猜想数列{an}的通项公式(不需要证明);
(Ⅱ)在数列{bn}中,若b1>b2>…bs(s≥3,且s∈N*),试用a1,b1表示bk,k∈{1,2,…,s};
(Ⅲ)在(Ⅰ)的条件下,设数列{cn}(n∈N*)满足c1=
,cn≠0,cn+1=-
cn2+cn (其中m为给定的不小于2的整数),求证:当n≤m时,恒有cn<1.
查看习题详情和答案>>
| ak-1+bk-1 |
| 2 |
| ak-1+bk-1 |
| 2 |
(Ⅰ)若a1=-1,b1=1,,求a2,a3,a4,并猜想数列{an}的通项公式(不需要证明);
(Ⅱ)在数列{bn}中,若b1>b2>…bs(s≥3,且s∈N*),试用a1,b1表示bk,k∈{1,2,…,s};
(Ⅲ)在(Ⅰ)的条件下,设数列{cn}(n∈N*)满足c1=
| 1 |
| 2 |
| 22-m |
| mam |
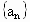 中,
中,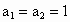 ,当
,当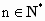 时,满足
时,满足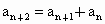 ,且设
,且设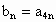 ,求证:
,求证: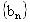 各项均为3的倍数.
各项均为3的倍数.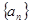 中,
中,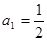 ,
,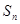 是其前
是其前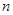 项和,且
项和,且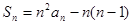
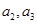 ;(II)证明:数列
;(II)证明:数列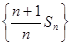 是等差数列;
是等差数列;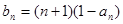 ,记数列
,记数列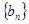 的前
的前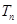 .求证:当
.求证:当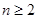 时,
时, 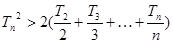 。
。 中,
中,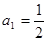 ,
,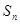 是其前
是其前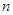 项和,且
项和,且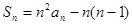
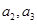 ;(II)证明:数列
;(II)证明:数列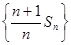 是等差数列;
是等差数列;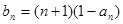 ,记数列
,记数列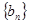 的前
的前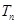 .求证:当
.求证:当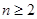 时,
时, 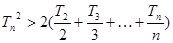 。
。