题目内容
(12分)已知在数列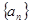 中,
中,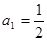 ,
,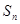 是其前
是其前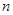 项和,且
项和,且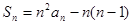
(I)求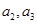 ;(II)证明:数列
;(II)证明:数列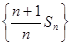 是等差数列;
是等差数列;
(III)令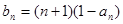 ,记数列
,记数列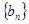 的前
的前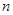 项和为
项和为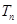 .求证:当
.求证:当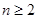 时,
时, 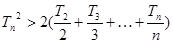 。
。
【答案】
(I)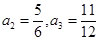 ;(II)见解析; (III)见解析.
;(II)见解析; (III)见解析.
【解析】(1)令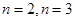 ,代入
,代入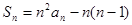 可求出
可求出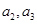 ;
;
(2)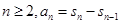 代入
代入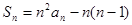 整理得
整理得 ,所以数列
,所以数列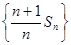 是等差数列;
是等差数列;
(3)由(1),(2)可求得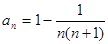 ,
,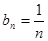 。所以
。所以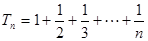 。当
。当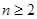 时,
时,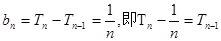 ;两边平方整理得
;两边平方整理得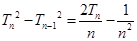 。叠加得
。叠加得
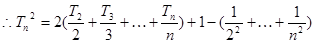 ,放缩求得
,放缩求得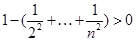 ,即证得结论。
,即证得结论。
(I)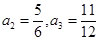 ;
;
(II)由条件可得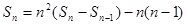 ,
,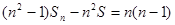
两边同除以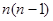 ,得:
,得:
所以:数列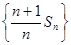 成等差数列,且首项和公差均为1
成等差数列,且首项和公差均为1
(III)由(Ⅰ)可得: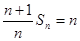 ,
,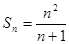 ,代入
,代入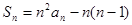 可得
可得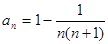 ,所以
,所以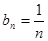 ,
,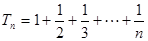 .
.
当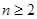 时,
时,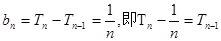
平方则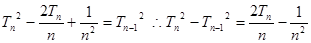
叠加得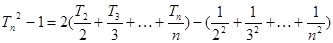
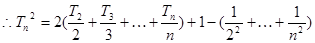
又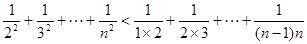
=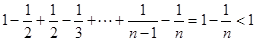
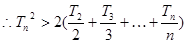

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
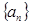 中,
中,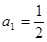 ,
,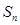 是其前
是其前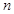 项和,且
项和,且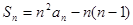 .
.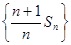 是等差数列;
是等差数列;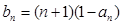 ,记数列
,记数列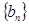 的前
的前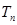 .
. 时,
时,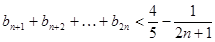
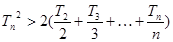
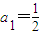 ,Sn是其前n项和,且Sn=n2an-n(n-1).
,Sn是其前n项和,且Sn=n2an-n(n-1).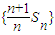 是等差数列;
是等差数列;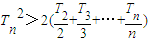 ;
;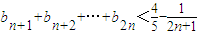 .
.