题目内容
在数列
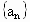 中,
中,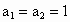 ,当
,当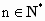 时,满足
时,满足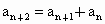 ,且设
,且设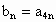 ,求证:
,求证: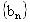 各项均为3的倍数.
各项均为3的倍数.
答案:略
解析:
提示:
解析:
|
证明: (1)∵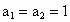 ,故 ,故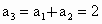 , , ,∴ ,∴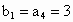 ,当n=1时, ,当n=1时,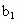 能被3整除. 能被3整除.
(2) 假设n=k时,即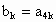 是3的倍数. 是3的倍数.
则 n=k+1时,
由归纳假设, 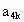 是3的倍数,故可知 是3的倍数,故可知 是3的倍数. 是3的倍数.
∴ n=k+1时,命题正确.综合 (1)、(2)可知,对任意正整数n,数列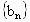 的各项都是3的倍数. 的各项都是3的倍数.
|
提示:
|
解析:由于要证的是与正整数 n有关的命题,可试用数学归纳法证之,这里要注意数列 |

练习册系列答案
相关题目
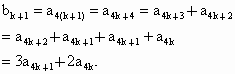
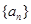 中,
中,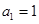 ,当
,当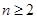 时,其前
时,其前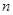 项和
项和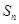 满足
满足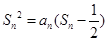 .
.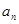 ;
;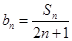 ,求数列
,求数列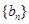 的前项和
的前项和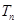 .
. 中,
中, ,当
,当 时,其前
时,其前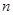 项和
项和 满足
满足 .
. ,求数列
,求数列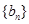 的前项和
的前项和 .
. ;
;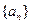 中,
中,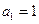 ,当
,当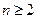 时,其前
时,其前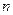 项和
项和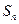 满足
满足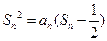 .
.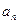 ;
;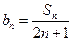 ,求数列
,求数列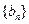 的前项和
的前项和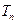 .
.