摘要:22.设若.求证: (1)且, (2)方程在(0.1)内有两个实根. 证明:(I)因为.所以. 由条件.消去.得, 由条件.消去.得.. 故.----------------7分 (II)抛物线的顶点坐标为. 在的两边乘以.得. 又因为而 所以方程在区间与内分别有一实根. 故方程在内有两个实根.-------------15分
网址:http://m.1010jiajiao.com/timu3_id_4454625[举报]
设A,B分别为椭圆
+
=1(a>b>0)的左、右顶点,C,D分别为椭圆上、下顶点,椭圆长半轴的长等于焦距,且四边形ACBD 的面积为4
.
(1)求椭圆的方程;
(2)设Q为椭圆上异于A、B的点,求证:直线QA与直线QB的斜率之积为定值;
(3)设P为直线x=
.(a2=b2+c2)上不同于点(
,0)的任意一点,若直线AP,BP分别与椭圆相交于异于A,B的点M、N,证明:点B在以MN为直径的圆内.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求椭圆的方程;
(2)设Q为椭圆上异于A、B的点,求证:直线QA与直线QB的斜率之积为定值;
(3)设P为直线x=
| a2 |
| c |
| a2 |
| c |
设A,B分别为椭圆 的左、右顶点,C,D分别为椭圆上、下顶点,椭圆长半轴的长等于焦距,且四边形ACBD 的面积为
的左、右顶点,C,D分别为椭圆上、下顶点,椭圆长半轴的长等于焦距,且四边形ACBD 的面积为 .
.
(1)求椭圆的方程;
(2)设Q为椭圆上异于A、B的点,求证:直线QA与直线QB的斜率之积为定值;
(3)设P为直线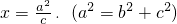 上不同于点(
上不同于点( ,0)的任意一点,若直线AP,BP分别与椭圆相交于异于A,B的点M、N,证明:点B在以MN为直径的圆内.
,0)的任意一点,若直线AP,BP分别与椭圆相交于异于A,B的点M、N,证明:点B在以MN为直径的圆内.
查看习题详情和答案>>
已知抛物线方程C:y2=2px(p>0),点F为其焦点,点N(3,1)在抛物线C的内部,设点M是抛物线C上的任意一点,|
|+|
|的最小值为4.
(1)求抛物线C的方程;
(2)过点F作直线l与抛物线C交于不同两点A、B,与y轴交于点P,且
=λ1
=λ2
,试判断λ1+λ2是否为定值?若是定值,求出该定值并证明;若不是定值,请说明理由.
查看习题详情和答案>>
| MF |
| MN |
(1)求抛物线C的方程;
(2)过点F作直线l与抛物线C交于不同两点A、B,与y轴交于点P,且
| PF |
| FA |
| FB |
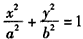 (a>b>0),A(0,b) 、B(0,-b)和 Q(a,0)为Γ的三个顶点。
(a>b>0),A(0,b) 、B(0,-b)和 Q(a,0)为Γ的三个顶点。 ,求点M的坐标;
,求点M的坐标; ,证明:E为CD的中点;
,证明:E为CD的中点; ?令a=10,b=5,点P的坐标是(-8,-1)。若椭圆Γ上的点P1、P2满足
?令a=10,b=5,点P的坐标是(-8,-1)。若椭圆Γ上的点P1、P2满足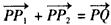 ,求点P1、P2的坐标。
,求点P1、P2的坐标。 ,A(0,b)、B(0,-b)和Q(a,0)为Γ的三个顶点.
,A(0,b)、B(0,-b)和Q(a,0)为Γ的三个顶点. ,求点M的坐标;
,求点M的坐标; ,证明:E为CD的中点;
,证明:E为CD的中点;
 ?令a=10,b=5,点P的坐标是(-8,-1),若椭圆Γ上的点P1、P2满足
?令a=10,b=5,点P的坐标是(-8,-1),若椭圆Γ上的点P1、P2满足 ,求点P1、P2的坐标.
,求点P1、P2的坐标.