Question

设A，B分别为椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的左、右顶点，C，D分别为椭圆上、下顶点，椭圆长半轴的长等于焦距，且四边形ACBD 的面积为4

3

．
（1）求椭圆的方程；
（2）设Q为椭圆上异于A、B的点，求证：直线QA与直线QB的斜率之积为定值；
（3）设P为直线x=

a2

c

 ．(a2=b2+c2)上不同于点（

a2

c

，0）的任意一点，若直线AP，BP分别与椭圆相交于异于A，B的点M、N，证明：点B在以MN为直径的圆内．

Answer 1

分析：（1）依题意寻找a，b，c，从而可求椭圆的方程；（2）先求直线QA与直线QB的斜率，利用椭圆的方程可得证；（3）要证点B在以MN为直径的圆内，只需证∠MBN为钝角，从而∠MBP为锐角，故即证

BM

•

BP

＞ 0．

解答：解：（1）依题意得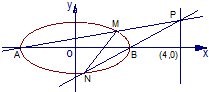，a=2c，2ab=4

3

，a2=b2+c2，∴a=2，c=1，b=

3

，∴椭圆的方程为

x2

4

+

y2

3

=1
（2）设Q（x，y），∵A（-2，0），B（2，0），∴KQA=

y

x+2

，KQB=

y

x-2

∴KQA•KQB=

y

x+2

•

y

x-2

=-

3

4

，故得证．
（3）由（1）得 A（-2，0），B（2，0），设M（x₀，y₀）
∵M在椭圆上，∴

y

2 0

=

3

4

(4-

x

2 0

)又点M异于顶点A，B，∴-2＜x₀＜2，由P，A，M三点共线可以得P(4，

6y0

x0+2

)，∴

BM

=(x0-2，y0)，

BP

=(2，

6y0

x0+2

)

BM

•

BP

=

2

x0+2

(

x

2 0

 -4+3

y

2 0

)，从而有

BM

•

BP

=

5

2

(2-x0)
∵-2＜x₀＜2，∴

BM

•

BP

＞ 0∴∠MBP为锐角，从而∠MBN为钝角，故点B在以MN为直径的圆内．

点评：本题主要考查椭圆标准方程的求解，考查椭圆方程的运用，考查等价转化的数学思想．