摘要:20.若存在实常数和.使得函数和对其定义域上的任意实数分别满足:和.则称直线为和的“隔离直线 .已知.(其中为自然对数的底数). (Ⅰ)求的极值, (Ⅱ) 函数和是否存在隔离直线?若存在.求出此隔离直线方程,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_4454497[举报]
(本小题满分13分)
设双曲线![]() ,点A、B分别为双曲线C实轴的左端点和虚轴的上端点,点
,点A、B分别为双曲线C实轴的左端点和虚轴的上端点,点![]() 、
、![]() 分别为双曲线C的左、右焦点,点M、N是双曲线C的右支上不同两点,点Q为线段MN的中点.已知在双曲线C上存在一点P,使得
分别为双曲线C的左、右焦点,点M、N是双曲线C的右支上不同两点,点Q为线段MN的中点.已知在双曲线C上存在一点P,使得![]() .
.
(Ⅰ)求双曲线C的离心率;
(Ⅱ)设![]() 为正常数,若点Q在直线
为正常数,若点Q在直线![]() 上,求直线MN在y轴上的截距的取值范围.
上,求直线MN在y轴上的截距的取值范围.
(本小题满分13分)
设数列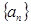 的前
的前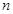 项和为
项和为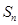 ,点
,点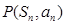 在直线
在直线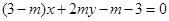 上,(
上,(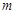 为常数,
为常数,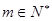 ,
,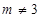 ).
).
(1)求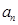 ;
;
(2)若数列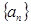 的公比
的公比 ,数列
,数列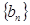 满足
满足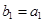 ,
,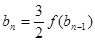 ,
,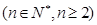 ,求证:
,求证: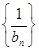 为等差数列,并求
为等差数列,并求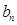 ;
;
(3)设数列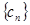 满足
满足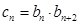 ,
,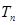 为数列
为数列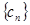 的前
的前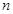 项和,且存在实数
项和,且存在实数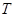 满足
满足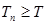
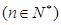 ,求
,求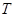 的最大值.
的最大值.
查看习题详情和答案>>
(本小题满分13分)
设数列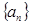 的前
的前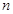 项和为
项和为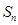 ,点
,点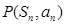 在直线
在直线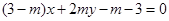 上,(
上,(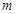 为常数,
为常数,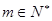 ,
,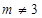 ).
).
(1)求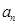 ;
;
(2)若数列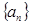 的公比
的公比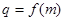 ,数列
,数列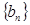 满足
满足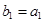 ,
,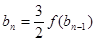 ,
,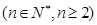 ,求证:
,求证: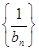 为等差数列,并求
为等差数列,并求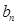 ;
;
(3)设数列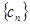 满足
满足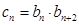 ,
,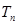 为数列
为数列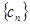 的前
的前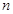 项和,且存在实数
项和,且存在实数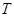 满足
满足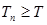
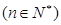 ,求
,求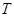 的最大值.
的最大值.
设数列
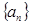 的前
的前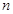 项和为
项和为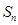 ,点
,点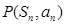 在直线
在直线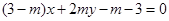 上,(
上,(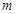 为常数,
为常数,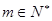 ,
,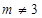 ).
).(1)求
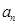 ;
;(2)若数列
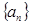 的公比
的公比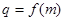 ,数列
,数列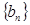 满足
满足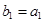 ,
,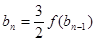 ,
,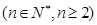 ,求证:
,求证: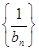 为等差数列,并求
为等差数列,并求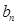 ;
;(3)设数列
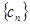 满足
满足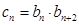 ,
,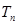 为数列
为数列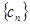 的前
的前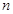 项和,且存在实数
项和,且存在实数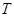 满足
满足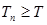
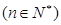 ,求
,求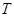 的最大值.
的最大值.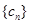 ,如果存在实常数
,如果存在实常数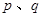 ,使得
,使得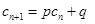 对于任意
对于任意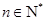 都成立,我们称数列
都成立,我们称数列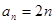 ,
,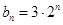 ,
,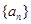 、
、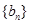 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数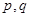 ,若不是,请说明理由;
,若不是,请说明理由;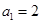 ,
, .
.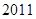 项的和.
项的和.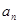 .
. )对于给定数列
)对于给定数列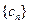 ,如果存在实常数
,如果存在实常数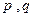 使得
使得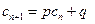 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列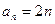 ,
,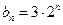 (
(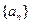 、
、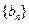 是否为“M类数列”?若是,指出它对应的实
是否为“M类数列”?若是,指出它对应的实 常数
常数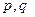 ,若不是,请说明理由;
,若不是,请说明理由; 列”,则数列
列”,则数列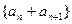 也是“M类数列”;
也是“M类数列”;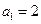 ,
,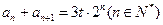 ,
,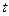 为常数,求数列
为常数,求数列 项的和,并判断
项的和,并判断