题目内容
(2002•岳阳)已知:如图,二次函数y=ax2+bx+c的图象与x轴、y轴都只有一个交点,分别为A、B且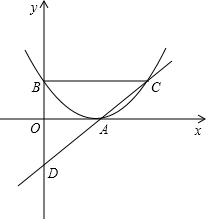 AB=2,又关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根互为相反数.
AB=2,又关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根互为相反数.
(1)求ac的值;
(2)求二次函数的解析式;
(3)过A点的直线与二次函数图象相交于另一个点C,与y轴的负半轴相交于点D,且使△ABD和△ABC的面积相等,求此直线的解析式并求△ABC的面积.
 AB=2,又关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根互为相反数.
AB=2,又关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根互为相反数.(1)求ac的值;
(2)求二次函数的解析式;
(3)过A点的直线与二次函数图象相交于另一个点C,与y轴的负半轴相交于点D,且使△ABD和△ABC的面积相等,求此直线的解析式并求△ABC的面积.
分析:(1)根据关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根x1,x2互为相反数,得出x1+x2=b+2ac=0,又由二次函数y=ax2+bx+c的图象与x轴只有一个交点,得出△=b2-4ac=0,联立可求ac及b的值;
(2)连接AB,由抛物线解析式可知OA=-
,OB=c,在Rt△AOB中,利用勾股定理求a的值,再求c的值,确定抛物线解析式;
(3)当△ABD和△ABC的面积相等时,△ABD和△BCD同底BD,则BD边上高的比为1:2,即A、C两点横坐标的比为1:2,根据A点横坐标可求C点横坐标,代入抛物线解析式求C点纵坐标,利用“两点法”可求直线AC的解析式.
(2)连接AB,由抛物线解析式可知OA=-
| b |
| 2a |
(3)当△ABD和△ABC的面积相等时,△ABD和△BCD同底BD,则BD边上高的比为1:2,即A、C两点横坐标的比为1:2,根据A点横坐标可求C点横坐标,代入抛物线解析式求C点纵坐标,利用“两点法”可求直线AC的解析式.
解答:解:(1)∵方程x2-(b+2ac)x+m=0(m<0)的两个实数根x1,x2互为相反数,
∴x1+x2=b+2ac=0…①,
又∵函数y=ax2+bx+c的图象与x轴只有一个交点,
∴△=b2-4ac=0…②,
解①②得ac=0(舍去),ac=1,
则b=±2,
根据对称轴x=-
>0且a>0可知b<0,故b=-2;
(2)连接AB,由抛物线解析式可知OA=-
,OB=c,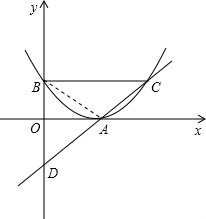
在Rt△AOB中,OA2+OB2=AB2,
即(-
)2+c2=22,
=4,
解得a=
(舍去负值),
则c=
=
,
所以,抛物线解析式为y=
x2-2x+
;
(3)∵y=
x2-2x+
=
(x-
)2,
∴A(
,0),
∵△ABD和△ABC的面积相等,
∴△ABD和△BCD的BD边上高的比为1:2,即A、C两点横坐标的比为1:2,
由此可得C点横坐标为2
,代入y=
(x-
)2中,得y=
,
则C(2
,
),
设直线AC解析式为y=kx+n,将A(
,0),C(2
,
)代入,得
,
解得
,
所以,直线AC解析式为y=x-
,
由于B(0,
),C(2
,
),
所以,S△ABC=
×2
×
=2.
∴x1+x2=b+2ac=0…①,
又∵函数y=ax2+bx+c的图象与x轴只有一个交点,
∴△=b2-4ac=0…②,
解①②得ac=0(舍去),ac=1,
则b=±2,
根据对称轴x=-
| b |
| 2a |
(2)连接AB,由抛物线解析式可知OA=-
| b |
| 2a |

在Rt△AOB中,OA2+OB2=AB2,
即(-
| b |
| 2a |
| b2+4a2c2 |
| 4a2 |
解得a=
| ||
| 2 |
则c=
| 1 |
| a |
| 2 |
所以,抛物线解析式为y=
| ||
| 2 |
| 2 |
(3)∵y=
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
∴A(
| 2 |
∵△ABD和△ABC的面积相等,
∴△ABD和△BCD的BD边上高的比为1:2,即A、C两点横坐标的比为1:2,
由此可得C点横坐标为2
| 2 |
| ||
| 2 |
| 2 |
| 2 |
则C(2
| 2 |
| 2 |
设直线AC解析式为y=kx+n,将A(
| 2 |
| 2 |
| 2 |
|
解得
|
所以,直线AC解析式为y=x-
| 2 |
由于B(0,
| 2 |
| 2 |
| 2 |
所以,S△ABC=
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查了二次函数的综合运用.关键是结合抛物线与x轴的交点只有一个,二元一次方程的两根互为相反数列出方程组求ac及b的值,根据三角形的面积关系求A、C两点横坐标的关系.

练习册系列答案
相关题目
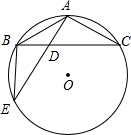 (2002•岳阳)已知:如图,△ABC内接于⊙O,AB=AC=
(2002•岳阳)已知:如图,△ABC内接于⊙O,AB=AC=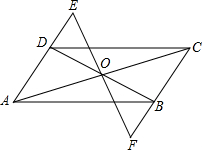 (2002•岳阳)如图,已知?ABCD的对角线AC、BD相交于点O,过点O任作一直线分别交AD、CB的延长线于E、F,求证:OE=OF.
(2002•岳阳)如图,已知?ABCD的对角线AC、BD相交于点O,过点O任作一直线分别交AD、CB的延长线于E、F,求证:OE=OF. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦,