摘要：(二)1.了解平面直角坐标系的有关概念,会由点的位置确定点的坐标,会由点的 坐标确定点的位置. 2.理解函数的意义,能根据一个具体的函数解析式,确定自变量的取值范围, 并会由自变量的值求出函数值. 3.掌握正比例函数.反比例函数.一次函数.二次函数的概念及性质,会画出 图象. 4.能根据不同条件,用待定系数法求函数解析式.
网址：http://m.1010jiajiao.com/timu3_id_445339[举报]
如图，平面直角坐标系的单位长度为小正方形的边长，△ABC在平面直角坐标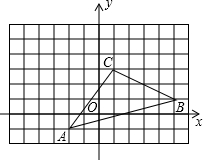
系中．
（1）请你写出△ABC各点的坐标；
（2）求△ABC的面积；
（3）若把△ABC向左平移3个单位，向上平移2个单位，得△A′B′C′，请你画出△A′B′C′，并写出△A′B′C′各点的坐标． 查看习题详情和答案>>
系中．（1）请你写出△ABC各点的坐标；
（2）求△ABC的面积；
（3）若把△ABC向左平移3个单位，向上平移2个单位，得△A′B′C′，请你画出△A′B′C′，并写出△A′B′C′各点的坐标． 查看习题详情和答案>>
已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形A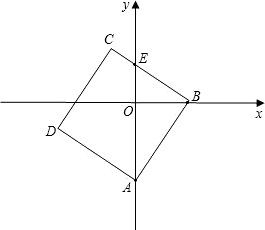
BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由． 查看习题详情和答案>>
BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由． 查看习题详情和答案>>
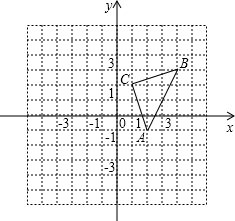如图，△ABC的顶点都在平面直角坐标系的网格上．
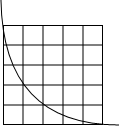（2012•永安市质检）如图，在平面直角坐标系的第一象限中有一个5×5的方形网络，每个小正方形的边长均为1个单位长，反比例函数y=