题目内容
已知:如图,点O是平面直角坐标系的原点,点A的坐标为(0,-4),点B为x轴上一动点,以线段AB为边作正方形ABCD(按逆时针方向标记),正方形ABCD随着点B的运动而随之相应变动.点E为y轴的正半轴与正方形A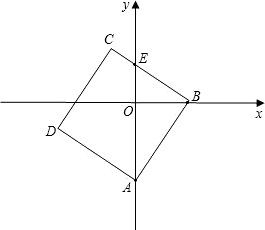 BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.
BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.(1)当t=3时,求点C的坐标;
(2)当t>0时,求m与t之间的函数关系式;
(3)是否存在t,使点M(-2,2)落在正方形ABCD的边上?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
分析:(1)由点C向x轴作垂线,构造△BFC≌△AOB,从而求出点C的坐标;
(2)分0<t≤4和t>4两种情况讨论,然后利用三角形相似求解;
(3)分t<0,0<t≤4和t>4三种情况讨论,结合图形进行解答.
(2)分0<t≤4和t>4两种情况讨论,然后利用三角形相似求解;
(3)分t<0,0<t≤4和t>4三种情况讨论,结合图形进行解答.
解答:解:(1)由点C向x轴作垂线,垂足为F,则△AOB≌△BFC,所以CF=BO=3,BF=OA=4,故点C的坐标为(-1,3)(3分)
(2)当0<t≤4时,CB与y轴交于点E,∵∠OBE+∠OBA=90°,∠OBE+∠OEB=90°,∴∠OEB=∠OBA,又∵∠AOB=∠BOE=90°,
∴△AOB∽△BOE,∴
=
,∴m=
t2;(5分)
当t>4时,CD与y轴交于点E,∵∠OAB+∠EAD=90°,∠DAE+∠DEA=90°,∴∠OAB=∠DEA,又∵∠AOB=∠ADE=90°,
∴△AOB∽△EDA,∴
=
,其中AB=AD=
,AE=m+4,OB=t,∴m=t+
-4;(7分)
故m=
;
(3)存在,
①当t≤0时
∵正方形ABCD位于x轴的下方(含x轴)∴此时不存在(8分)
②当0<t≤4时,
当点M在BC边上时,t=2,或t=-4(舍)(9分)
当点M在CD边上时,t=2,或t=4(10分)
③当t>4时,
当点M在CD边上时,t=2(舍);t=4(舍) (11分)
当点M在AD边上时,t=12 (12分)
综上所述:存在,符合条件的t的值为2、4、12.
(2)当0<t≤4时,CB与y轴交于点E,∵∠OBE+∠OBA=90°,∠OBE+∠OEB=90°,∴∠OEB=∠OBA,又∵∠AOB=∠BOE=90°,
∴△AOB∽△BOE,∴
| AO |
| BO |
| OB |
| OE |
| 1 |
| 4 |
当t>4时,CD与y轴交于点E,∵∠OAB+∠EAD=90°,∠DAE+∠DEA=90°,∴∠OAB=∠DEA,又∵∠AOB=∠ADE=90°,
∴△AOB∽△EDA,∴
| AB |
| AE |
| OB |
| AD |
| 16+t2 |
| 16 |
| t |
故m=
|
(3)存在,
①当t≤0时
∵正方形ABCD位于x轴的下方(含x轴)∴此时不存在(8分)
②当0<t≤4时,
当点M在BC边上时,t=2,或t=-4(舍)(9分)
当点M在CD边上时,t=2,或t=4(10分)
③当t>4时,
当点M在CD边上时,t=2(舍);t=4(舍) (11分)
当点M在AD边上时,t=12 (12分)
综上所述:存在,符合条件的t的值为2、4、12.
点评:解答本题要充分利用正方形的特殊性质.搞清楚B点运动时y轴与正方形边长的位置关系,及正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

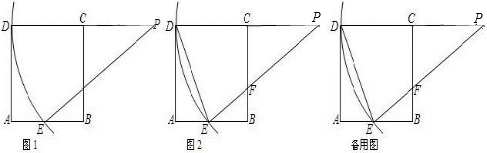
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
 ,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,要求写出计算过程)
,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,要求写出计算过程)
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.