摘要：例5如图5.在梯形ABCD中.AB∥CD...E为AD边上的任意一点.EF∥AB.且EF交BC于点F.某学生在研究这一问题时.发现如下事实: ①当时.有, ②当时.有, ③当时.有． 当时.参照上述研究结论.请你猜想用k表示DE的一般结论.并给出证明. 图5 分析:类比条件中的等式.可以猜想得:EF =． 证明:过点E作BC的平行线交AB于G.交CD的延长线于H． ∵AB∥CD.∴∽.∴. 又∥∥.∴. ∴.. ∴.可得．
网址：http://m.1010jiajiao.com/timu3_id_444694[举报]
（2013•扬州）如图1，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E．设BP=x，CE=y．
（1）求y与x的函数关系式；
（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；
（3）如图2，若m=4，将△PEC沿PE翻折至△PEG位置，∠BAG=90°，求BP长．
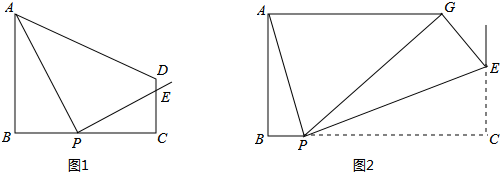
查看习题详情和答案>>
（1）求y与x的函数关系式；
（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；
（3）如图2，若m=4，将△PEC沿PE翻折至△PEG位置，∠BAG=90°，求BP长．
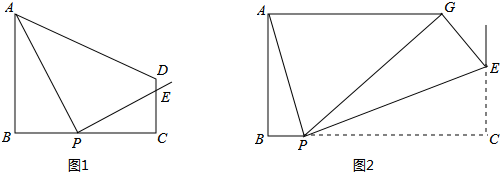
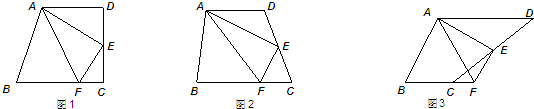
24、如图1，在梯形ABCD中，AD∥BC，∠C=90°，点E为CD的中点，点F在底边BC上，且∠FAE=∠DAE．
（1）请你通过观察、测量、猜想，得出∠AEF的度数；
（2）若梯形ABCD中，AD∥BC，∠C不是直角，点F在底边BC或其延长线上，如图2、图3，其他条件不变，你在（1）中得出的结论是否仍然成立，若都成立，请在图2、图3中选择其中一图进行证明；若不都成立，请说明理由．
查看习题详情和答案>>
（1）请你通过观察、测量、猜想，得出∠AEF的度数；
（2）若梯形ABCD中，AD∥BC，∠C不是直角，点F在底边BC或其延长线上，如图2、图3，其他条件不变，你在（1）中得出的结论是否仍然成立，若都成立，请在图2、图3中选择其中一图进行证明；若不都成立，请说明理由．
（2011•石家庄二模）如图1，在梯形ABCD中，AD∥BC，∠C=90°，点E从点B出发，以每秒k个单位长的速度，沿折线BA-AD-DC向点C运动；点F以每秒1个单位长的速度从点C向点B运动，点E、F同时出发同时停止．设运动时间为t秒时，△EBF的面积为y，已知y与t的函数关系如图2所示．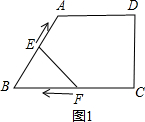
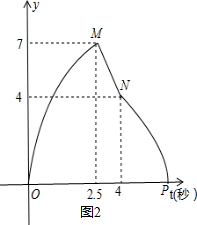
请根据图中的信息，解答下列问题：
（1）点E运动到A、D两点时，y的值分别是
（2）求BC和CD的长；
（3）求点E的运动速度k；
（4）当t为何值时，△EBF与梯形ABCD的面积之比是1：3．
查看习题详情和答案>>
请根据图中的信息，解答下列问题：
（1）点E运动到A、D两点时，y的值分别是
7
7
和4
4
；（2）求BC和CD的长；
（3）求点E的运动速度k；
（4）当t为何值时，△EBF与梯形ABCD的面积之比是1：3．
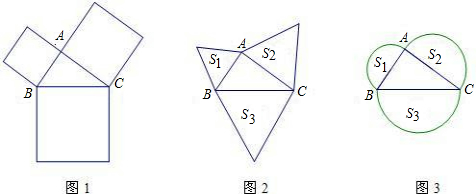
勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成（图1：△ABC中，∠BAC=90°）．
请解答：
（1）如图2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S1、S2、S3之间的数量关系是 ．
（2）如图3，若以直角三角形的三边为直径向外作半圆，则它们的面积S1、S2、S3之间的数量关系是 ，请说明理由．
（3）如图4，在梯形ABCD中，AD∥BC，∠ABC+∠BCD=90°，BC=2AD，分别以AB、CD、AD为边向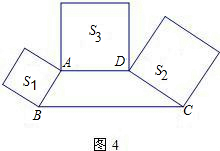
梯形外作正方形，其面积分别为S1、S2、S3，则S1、S2、S3之间的数量关系式为 ，请说明理由．
查看习题详情和答案>>
请解答：
（1）如图2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S1、S2、S3之间的数量关系是
（2）如图3，若以直角三角形的三边为直径向外作半圆，则它们的面积S1、S2、S3之间的数量关系是
（3）如图4，在梯形ABCD中，AD∥BC，∠ABC+∠BCD=90°，BC=2AD，分别以AB、CD、AD为边向
梯形外作正方形，其面积分别为S1、S2、S3，则S1、S2、S3之间的数量关系式为阅读材料：
如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为点O．
求证：S四边形ABCD=
AC•BD；
证明：∵AC⊥BD，
∴S四边形ABCD=S△ACD+S△ACB=
AC•OD+
AC•BO=
AC（OD+OB）=
AC•BD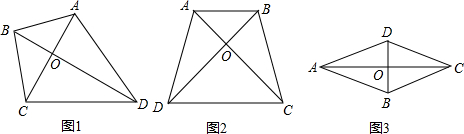
解答下列问题：
（1）上述证明得到的结论可叙述为
（2）如图2，在梯形ABCD中，AB∥CD，AD=BC，AC⊥BD，且AC=8，则S梯形ABCD=
（3）如图3，在菱形ABCD中，AB=5，AC=8，则S菱形ABCD=
查看习题详情和答案>>
如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为点O．
求证：S四边形ABCD=
| 1 |
| 2 |
证明：∵AC⊥BD，
∴S四边形ABCD=S△ACD+S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答下列问题：
（1）上述证明得到的结论可叙述为
对角线互相垂直的四边形的面积等于对角线乘积的一半
对角线互相垂直的四边形的面积等于对角线乘积的一半
；（2）如图2，在梯形ABCD中，AB∥CD，AD=BC，AC⊥BD，且AC=8，则S梯形ABCD=
32
32
；（3）如图3，在菱形ABCD中，AB=5，AC=8，则S菱形ABCD=
24
24
．