题目内容
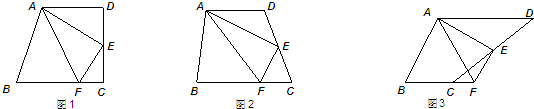
24、如图1,在梯形ABCD中,AD∥BC,∠C=90°,点E为CD的中点,点F在底边BC上,且∠FAE=∠DAE.
(1)请你通过观察、测量、猜想,得出∠AEF的度数;
(2)若梯形ABCD中,AD∥BC,∠C不是直角,点F在底边BC或其延长线上,如图2、图3,其他条件不变,你在(1)中得出的结论是否仍然成立,若都成立,请在图2、图3中选择其中一图进行证明;若不都成立,请说明理由.
(1)请你通过观察、测量、猜想,得出∠AEF的度数;
(2)若梯形ABCD中,AD∥BC,∠C不是直角,点F在底边BC或其延长线上,如图2、图3,其他条件不变,你在(1)中得出的结论是否仍然成立,若都成立,请在图2、图3中选择其中一图进行证明;若不都成立,请说明理由.

分析:(1)根据图象观察或测量得到∠AEF的度数即可;
(2)延长AE交BC的延长线于点G,根据平行线的性质得到∠D=∠ECG,∠DAE=∠G,根据AAS证出△ADE≌△GCE,推出AE=GE,证出FA=FG,根据等腰三角形的性质即可推出答案.
(2)延长AE交BC的延长线于点G,根据平行线的性质得到∠D=∠ECG,∠DAE=∠G,根据AAS证出△ADE≌△GCE,推出AE=GE,证出FA=FG,根据等腰三角形的性质即可推出答案.
解答: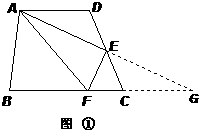 解:(1)∠AEF的度数是90°.
解:(1)∠AEF的度数是90°.
(2)都成立.以图2为例证明.
证明:如图①,延长AE交BC的延长线于点G,
∵AD∥BC,
∴∠D=∠ECG,∠DAE=∠G,
∵E为DC的中点,
∴DE=EC,
∴△ADE≌△GCE(AAS),
∴AE=GE,
∵∠FAE=∠DAE,
∴∠FAE=∠G,
∴FA=FG,
∴EF⊥AE.
∴∠AEF=90°.
 解:(1)∠AEF的度数是90°.
解:(1)∠AEF的度数是90°.(2)都成立.以图2为例证明.
证明:如图①,延长AE交BC的延长线于点G,
∵AD∥BC,
∴∠D=∠ECG,∠DAE=∠G,
∵E为DC的中点,
∴DE=EC,
∴△ADE≌△GCE(AAS),
∴AE=GE,
∵∠FAE=∠DAE,
∴∠FAE=∠G,
∴FA=FG,
∴EF⊥AE.
∴∠AEF=90°.
点评:本题主要考查对等腰三角形的性质和判定,全等三角形的性质和判定,平行线的性质,梯形的性质等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
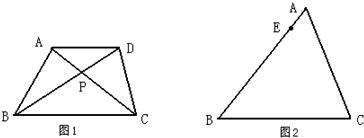

 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是

