题目内容
(2013•扬州)如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.
(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
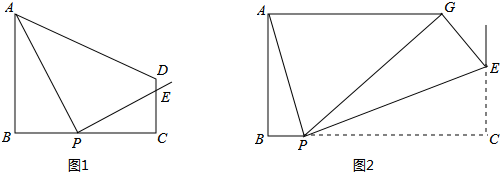
(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
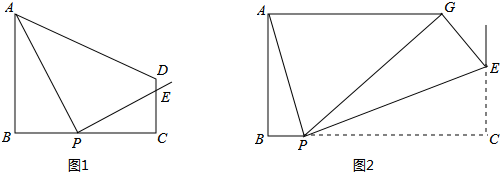
分析:(1)证明△ABP∽△PCE,利用比例线段关系求出y与x的函数关系式;
(2)根据(1)中求出的y与x的关系式,利用二次函数性质,求出其最大值,列不等式确定m的取值范围;
(3)根据翻折的性质及已知条件,构造直角三角形,利用勾股定理求出BP的长度.解答中提供了三种解法,可认真体会.
(2)根据(1)中求出的y与x的关系式,利用二次函数性质,求出其最大值,列不等式确定m的取值范围;
(3)根据翻折的性质及已知条件,构造直角三角形,利用勾股定理求出BP的长度.解答中提供了三种解法,可认真体会.
解答:解:(1)∵∠APB+∠CPE=90°,∠CEP+∠CPE=90°,
∴∠APB=∠CEP,又∵∠B=∠C=90°,
∴△ABP∽△PCE,
∴
=
,即
=
,
∴y=-
x2+
x.
(2)∵y=-
x2+
x=-
(x-
)2+
,
∴当x=
时,y取得最大值,最大值为
.
∵点P在线段BC上运动时,点E总在线段CD上,
∴
≤1,解得m≤2
.
∴m的取值范围为:0<m≤2
.
(3)由折叠可知,PG=PC,EG=EC,∠GPE=∠CPE,
又∵∠GPE+∠APG=90°,∠CPE+∠APB=90°,
∴∠APG=∠APB.
∵∠BAG=90°,∴AG∥BC,
∴∠GAP=∠APB,
∴∠GAP=∠APG,
∴AG=PG=PC.

解法一:如解答图所示,分别延长CE、AG,交于点H,
则易知ABCH为矩形,HE=CH-CE=2-y,GH=AH-AG=4-(4-x)=x,
在Rt△GHE中,由勾股定理得:GH2+HE2=GE2,
即:x2+(2-y)2=y2,化简得:x2-4y+4=0 ①
由(1)可知,y=-
x2+
x,这里m=4,∴y=-
x2+2x,
代入①式整理得:3x2-8x+4=0,解得:x=
或x=2,
∴BP的长为
或2.
解法二:如解答图所示,连接GC.
∵AG∥PC,AG=PC,
∴四边形APCG为平行四边形,∴AP=CG.
易证△ABP≌GNC,∴CN=BP=x.
过点G作GN⊥PC于点N,则GN=2,PN=PC-CN=4-2x.
在Rt△GPN中,由勾股定理得:PN2+GN2=PG2,
即:(4-2x)2+22=(4-x)2,
整理得:x2-8x+4=0,解得:x=
或x=2,
∴BP的长为
或2.
解法三:过点A作AK⊥PG于点K,
∵∠APB=∠APG,
∴AK=AB.
易证△APB≌△APK,
∴PK=BP=x,
∴GK=PG-PK=4-2x.
在Rt△AGK中,由勾股定理得:GK2+AK2=AG2,
即:(4-2x)2+22=(4-x)2,
整理得:3x2-8x+4=0,
解得:x=
或x=2,
∴BP的长为
或2.
∴∠APB=∠CEP,又∵∠B=∠C=90°,
∴△ABP∽△PCE,
∴
| AB |
| PC |
| BP |
| CE |
| 2 |
| m-x |
| x |
| y |
∴y=-
| 1 |
| 2 |
| m |
| 2 |
(2)∵y=-
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| m2 |
| 8 |
∴当x=
| m |
| 2 |
| m2 |
| 8 |
∵点P在线段BC上运动时,点E总在线段CD上,
∴
| m2 |
| 8 |
| 2 |
∴m的取值范围为:0<m≤2
| 2 |
(3)由折叠可知,PG=PC,EG=EC,∠GPE=∠CPE,
又∵∠GPE+∠APG=90°,∠CPE+∠APB=90°,
∴∠APG=∠APB.
∵∠BAG=90°,∴AG∥BC,
∴∠GAP=∠APB,
∴∠GAP=∠APG,
∴AG=PG=PC.

解法一:如解答图所示,分别延长CE、AG,交于点H,
则易知ABCH为矩形,HE=CH-CE=2-y,GH=AH-AG=4-(4-x)=x,
在Rt△GHE中,由勾股定理得:GH2+HE2=GE2,
即:x2+(2-y)2=y2,化简得:x2-4y+4=0 ①
由(1)可知,y=-
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
代入①式整理得:3x2-8x+4=0,解得:x=
| 2 |
| 3 |
∴BP的长为
| 2 |
| 3 |
解法二:如解答图所示,连接GC.
∵AG∥PC,AG=PC,
∴四边形APCG为平行四边形,∴AP=CG.
易证△ABP≌GNC,∴CN=BP=x.
过点G作GN⊥PC于点N,则GN=2,PN=PC-CN=4-2x.
在Rt△GPN中,由勾股定理得:PN2+GN2=PG2,
即:(4-2x)2+22=(4-x)2,
整理得:x2-8x+4=0,解得:x=
| 2 |
| 3 |
∴BP的长为
| 2 |
| 3 |
解法三:过点A作AK⊥PG于点K,
∵∠APB=∠APG,
∴AK=AB.
易证△APB≌△APK,
∴PK=BP=x,
∴GK=PG-PK=4-2x.
在Rt△AGK中,由勾股定理得:GK2+AK2=AG2,
即:(4-2x)2+22=(4-x)2,
整理得:3x2-8x+4=0,
解得:x=
| 2 |
| 3 |
∴BP的长为
| 2 |
| 3 |
点评:本题是代数几何综合题,考查了全等三角形、相似三角形、勾股定理、梯形、矩形、折叠、函数关系式、二次函数最值等知识点,所涉及考点众多,有一定的难度.注意第(2)问中求m取值范围时二次函数性质的应用,以及第(3)问中构造直角三角形的方法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 (2013•扬州)如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BC=12,∠ABC=60°,则梯形ABCD的周长为
(2013•扬州)如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BC=12,∠ABC=60°,则梯形ABCD的周长为 (2013•扬州)如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在
(2013•扬州)如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在
 (2013•扬州)如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为
(2013•扬州)如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为 (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.