题目内容
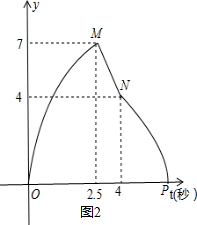
(2011•石家庄二模)如图1,在梯形ABCD中,AD∥BC,∠C=90°,点E从点B出发,以每秒k个单位长的速度,沿折线BA-AD-DC向点C运动;点F以每秒1个单位长的速度从点C向点B运动,点E、F同时出发同时停止.设运动时间为t秒时,△EBF的面积为y,已知y与t的函数关系如图2所示.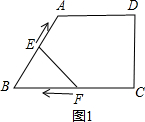
请根据图中的信息,解答下列问题:
(1)点E运动到A、D两点时,y的值分别是
(2)求BC和CD的长;
(3)求点E的运动速度k;
(4)当t为何值时,△EBF与梯形ABCD的面积之比是1:3.


请根据图中的信息,解答下列问题:
(1)点E运动到A、D两点时,y的值分别是
7
7
和4
4
;(2)求BC和CD的长;
(3)求点E的运动速度k;
(4)当t为何值时,△EBF与梯形ABCD的面积之比是1:3.
分析:(1)根据图2可以得到OM表示E在BA段,MN表示E在AD段,NP表示E在DC段,据此即可判断;
(2)根据E在A点和D点时,△EBF的面积分别是7和4,利用面积公式即可得到关于CD和BC的方程组,即可求得BC和CD的长;
(3)根据两个点的运动时间以及(2)中求得的运动距离,即可求得运动的速度;
(4)首先求得梯形ABCD的面积,当E在AB上时,过点E作EH⊥BC于点H,△EBH∽△ABG,根据相似三角形的对应边的比相等,即可得到关于时间的方程,从而求解.
(2)根据E在A点和D点时,△EBF的面积分别是7和4,利用面积公式即可得到关于CD和BC的方程组,即可求得BC和CD的长;
(3)根据两个点的运动时间以及(2)中求得的运动距离,即可求得运动的速度;
(4)首先求得梯形ABCD的面积,当E在AB上时,过点E作EH⊥BC于点H,△EBH∽△ABG,根据相似三角形的对应边的比相等,即可得到关于时间的方程,从而求解.
解答: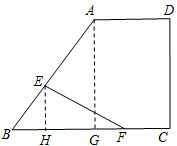 解:(1)点E运动到A、D两点时,在图2中对应的点是M,N两点,则对应的值是:7和4;
解:(1)点E运动到A、D两点时,在图2中对应的点是M,N两点,则对应的值是:7和4;
(2)当t=2.5秒时,△EBF的面积为y=
•(BC-CF)•CD=7,
即:
(BC-
)•CD=7.
当t=4秒时,△EBF的面积为y=
•(BC-CF)•CD=4,
即:
(BC-4)•CD=4.
∴
…6分
(3)法一:
∵BC=6,点F的速度是每秒1个单位,
∴BC=6,
∴点E从D运动到C用时为6-4=2秒,
又∵CD=4,
∴点E的运动速度为每秒2个单位.…9分
法二:如图,过点A作AG⊥BC于点G,
∵AB=2.5k,AD=1.5k,∴BG=6-1.5 k,
在Rt△ABG中,42+(6-1.5k)2=(2.5k)2.
∴k1=2,k2=-6.5(不合题意舍去),
即点E的运动速度为每秒2个单位.
(4)∵k=2,∴AD=3,AB=5,∴S△EBF=6,S梯形ABCD=18.
由题意可知运动过程中有两个时刻△EBF的面积等于6.
①当E在AB上时,过点E作EH⊥BC于点H,
△EBH∽△ABG,
∴
=
,
∴EH=
t,
∴
×
t×(6-t)=6,解得t=
,∵t≤2.5.
∴t=
②当E在AD上时,
×4×(6-t)=6,解得t=3.
综上所述,当t=
或t=3秒时,△EBF与梯形ABCD的面积之比为1:3.
 解:(1)点E运动到A、D两点时,在图2中对应的点是M,N两点,则对应的值是:7和4;
解:(1)点E运动到A、D两点时,在图2中对应的点是M,N两点,则对应的值是:7和4;(2)当t=2.5秒时,△EBF的面积为y=
| 1 |
| 2 |
即:
| 1 |
| 2 |
| 5 |
| 2 |
当t=4秒时,△EBF的面积为y=
| 1 |
| 2 |
即:
| 1 |
| 2 |
∴
|
(3)法一:
∵BC=6,点F的速度是每秒1个单位,
∴BC=6,
∴点E从D运动到C用时为6-4=2秒,
又∵CD=4,
∴点E的运动速度为每秒2个单位.…9分
法二:如图,过点A作AG⊥BC于点G,
∵AB=2.5k,AD=1.5k,∴BG=6-1.5 k,
在Rt△ABG中,42+(6-1.5k)2=(2.5k)2.
∴k1=2,k2=-6.5(不合题意舍去),
即点E的运动速度为每秒2个单位.
(4)∵k=2,∴AD=3,AB=5,∴S△EBF=6,S梯形ABCD=18.
由题意可知运动过程中有两个时刻△EBF的面积等于6.
①当E在AB上时,过点E作EH⊥BC于点H,
△EBH∽△ABG,
∴
| BE |
| AB |
| EH |
| AG |
∴EH=
| 8 |
| 5 |
∴
| 1 |
| 2 |
| 8 |
| 5 |
6±
| ||
| 2 |
∴t=
6-
| ||
| 2 |
②当E在AD上时,
| 1 |
| 2 |
综上所述,当t=
6-
| ||
| 2 |
点评:本题考查了相似三角形的判定与性质,正确利用题目中的图形的关系,转化成方程问题求解是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目