摘要:25. 图14-1至图14-7的正方形霓虹灯广告牌ABCD都是20×20的等距网格(每个小方格的边长均为1个单位长).其对称中心为点O. 如图14-1.有一个边长为6个单位长的正方形EFGH的对称中心也是点O.它以每秒1个单位长的速度由起始位置向外扩大(即点O不动.正方形EFGH经过一秒由6×6扩大为8×8,再经过一秒.由8×8扩大为10×10,--).直到充满正方形ABCD.再以同样的速度逐步缩小到起始时的大小.然后一直不断地以同样速度再扩大.再缩小. 另有一个边长为6个单位长的正方形MNPQ从如图14-1所示的位置开始.以每秒1个单位长的速度.沿正方形ABCD的内侧边缘按A→B→C→D→A移动(即正方形MNPQ从点P与点A重合位置开始.先向左平移.当点Q与点B重合时.再向上平移.当点M与点C重合时.再向右平移.当点N与点D重合时.再向下平移.到达起始位置后仍继续按上述方式移动). 正方形EFGH和正方形MNPQ从如图14-1的位置同时开始运动.设运动时间为x秒.它们的重叠部分面积为y个平方单位. (1)请你在图14-2和图14-3中分别画出x为2秒.18秒时.正方形EFGH和正方形MNPQ的位置及重叠部分.并分别写出重叠部分的面积, (2)①如图14-4.当1≤x≤3.5时.求y与x的函数关系式, ②如图14-5.当3.5≤x≤7时.求y与x的函数关系式, ③如图14-6.当7≤x≤10.5时.求y与x的函数关系式, ④如图14-7.当10.5≤x≤13时.求y与x的函数关系式. (3)对于正方形MNPQ在正方形ABCD各边上移动一周的过程.请你根据重叠部分面积y的变化情况.指出y取得最大值和最小值时.相对应的x的取值情况.并指出最大值和最小值分别是多少.是额外加分题.加分幅度为1-4分) D 图14-2 图14-3 2006年河北省课程改革实验区初中毕业生升学考试
网址:http://m.1010jiajiao.com/timu3_id_444212[举报]
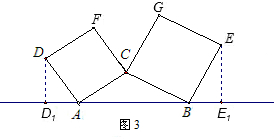
如图(1)至图(3),C为定线段AB外一动点,以AC、BC为边分别向外侧作正方形CADF和正方形CBEG,分别作DD1⊥AB、EE1⊥AB,垂足分别为D1、E1.当C的位置在直线AB的同侧变化过程中,
(1)如图(1),当∠ACB=90°,AC=4,BC=3时,求DD1+EE1的值;
(2)求证:不论C的位置在直线AB的同侧怎样变化,DD1+EE1的值为定值;
(3)求证:不论C的位置在直线AB的同侧怎样变化,线段DE的中点M为定点.

 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图(1),当∠ACB=90°,AC=4,BC=3时,求DD1+EE1的值;
(2)求证:不论C的位置在直线AB的同侧怎样变化,DD1+EE1的值为定值;
(3)求证:不论C的位置在直线AB的同侧怎样变化,线段DE的中点M为定点.

 查看习题详情和答案>>
查看习题详情和答案>>
(2011•葫芦岛)如图(1)至图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,点B、C、E在同一条直线上.
(1)已知:如图(1),AC=AB,AD=AE.求证:①CD=BE;②CD⊥BE.
(2)如图(2),当AB=kAC,AE=kAD(k≠1)时,分别说出(1)中的两个 予证明;若不成立,请说明理由.
予证明;若不成立,请说明理由.
查看习题详情和答案>>
(1)已知:如图(1),AC=AB,AD=AE.求证:①CD=BE;②CD⊥BE.
(2)如图(2),当AB=kAC,AE=kAD(k≠1)时,分别说出(1)中的两个
②
②
结论是否成立,若成立,请给 予证明;若不成立,请说明理由.
予证明;若不成立,请说明理由.如图(1),小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图(2)),量得他们的斜边长为10cm,较小锐角为30.再将这两张三角纸片摆成如图(3)的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图(3)至图(6)中统一用F表示)
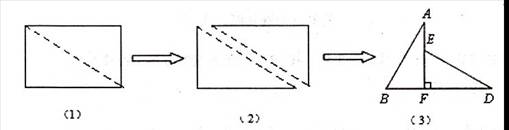
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
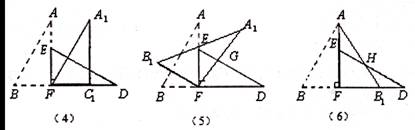
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A.F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB,交DE丁点H,请证明:AH=DH.
查看习题详情和答案>>
如图(1),小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图(2)),量得他们的斜边长为10cm,较小锐角为30.再将这两张三角纸片摆成如图(3)的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图(3)至图(6)中统一用F表示)
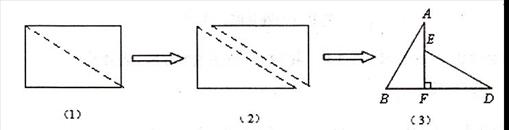
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A.F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB,交DE丁点H,请证明:AH=DH.


小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A.F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB,交DE丁点H,请证明:AH=DH.

