摘要：23．如图.∠BAC =.在CB的延长线上分别取点D.E.使∠DAB =∠BAE =∠C.求证:
网址：http://m.1010jiajiao.com/timu3_id_443493[举报]
如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM=
BD，EN=
CE，得到图③，请解答下列问题：
（1）若AB=AC，请探究下列数量关系：
①在图②中，BD与CE的数量关系是 ；
②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；
（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC的数量关系，直接写出你的猜想，不必证明． 查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
（1）若AB=AC，请探究下列数量关系：
①在图②中，BD与CE的数量关系是
②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；
（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC的数量关系，直接写出你的猜想，不必证明． 查看习题详情和答案>>
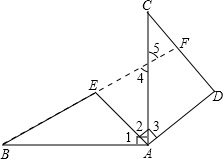推理填空如图，∠BAC=∠DAE=90°，AC=AB，AE=AD，试说明BE⊥CD．
证明：∵∠BAC=∠DAE=90°（已知）
即∠1+∠2=90°，∠2+∠3=90°
∴∠1=∠3（
在△DAC与△EAB中
|
∴△DAC≌△EAB（
∴∠B=∠C（
又∵∠4=∠5（
且∠B+∠4=90°（
∴∠C+∠5=90°
即BE⊥CD． 查看习题详情和答案>>
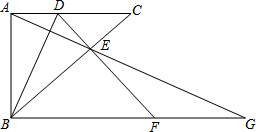（2013•松江区二模）如图，已知在Rt△ABC中，∠BAC=90°，AB=4，点D在边AC上，△ABD沿BD翻折，点A与BC边上的点E重合，过点B作BG∥AC交AE的延长线于点G，交DE的延长线于点F．（1）当∠ABC=60°时，求CD的长；
（2）如果AC=x，AD=y，求y关于x的函数解析式，并写出函数定义域；
（3）联结CG，如果∠ACB=∠CGB，求AC的长．
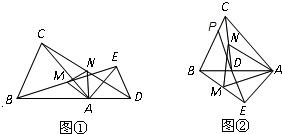25、已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．
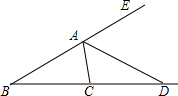如图所示，在△ABC中，∠B=