题目内容
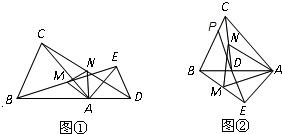 25、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
25、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;
(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;
(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.
分析:(1)因为∠BAC=∠DAE,所以∠BAE=∠CAD,又因为AB=AC,AD=AE,利用SAS可证出△BAE≌△CAD,可知BE、CD是对应边,根据全等三角形对应边上的中线相等,可证△AMN是等腰三角形.
(2)利用(1)中的证明方法仍然可以得出(1)中的结论,思路不变.
(3)先证出△ABM≌△ACN(SAS),可得出∠CAN=∠BAM,所以∠BAC=∠MAN(等角加等角和相等),又∵∠BAC=∠DAE,所以∠MAN=∠DAE=∠BAC,所以△AMN,△ADE和△ABC都是顶角相等的等腰三角形,所以∠PBD=∠AMN,所以△PBD∽△AMN(两个角对应相等,两三角形相似).
(2)利用(1)中的证明方法仍然可以得出(1)中的结论,思路不变.
(3)先证出△ABM≌△ACN(SAS),可得出∠CAN=∠BAM,所以∠BAC=∠MAN(等角加等角和相等),又∵∠BAC=∠DAE,所以∠MAN=∠DAE=∠BAC,所以△AMN,△ADE和△ABC都是顶角相等的等腰三角形,所以∠PBD=∠AMN,所以△PBD∽△AMN(两个角对应相等,两三角形相似).
解答:证明:(1)①∵∠BAC=∠DAE∴∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△ABE≌△ACD,
∴BE=CD.
②由△ABE≌△ACD,得
∠ABE=∠ACD,BE=CD,
∵M、N分别是BE,CD的中点,
∴BM=CN.
又∵AB=AC,
∴△ABM≌△ACN.
∴AM=AN,即△AMN为等腰三角形.
(2)(1)中的两个结论仍然成立.
(3)在图②中正确画出线段PD,
由(1)同理可证△ABM≌△ACN,
∴∠CAN=∠BAM∴∠BAC=∠MAN.
又∵∠BAC=∠DAE,
∴∠MAN=∠DAE=∠BAC.
∴△AMN,△ADE和△ABC都是顶角相等的等腰三角形.
∴∠PBD=∠AMN,
∴△PBD∽△AMN.
∵AB=AC,AD=AE,
∴△ABE≌△ACD,
∴BE=CD.
②由△ABE≌△ACD,得
∠ABE=∠ACD,BE=CD,
∵M、N分别是BE,CD的中点,
∴BM=CN.
又∵AB=AC,
∴△ABM≌△ACN.
∴AM=AN,即△AMN为等腰三角形.
(2)(1)中的两个结论仍然成立.
(3)在图②中正确画出线段PD,
由(1)同理可证△ABM≌△ACN,
∴∠CAN=∠BAM∴∠BAC=∠MAN.
又∵∠BAC=∠DAE,
∴∠MAN=∠DAE=∠BAC.
∴△AMN,△ADE和△ABC都是顶角相等的等腰三角形.
∴∠PBD=∠AMN,
∴△PBD∽△AMN.
点评:本题利用了全等三角形的判定和性质,以及等腰三角形一个顶角相等,则底角相等的性质,还有相似三角形的判定(两个角对应相等的两个三角形相似).

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
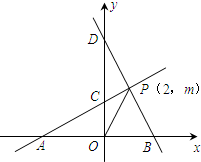 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
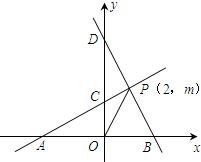 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.