摘要：在平面直角坐标系中.A.B两点的坐标分别为．点P从A点开始以2cm／s的速度沿折线AOy运动.同时点Q从B点开始以1cm/s的速度沿折线BOy运动． (1)在运动开始后的每一时刻一定存在以A.O.P为顶点的三角形和以B.O.Q为顶点的三角形吗?如果存在.那么以A.O.P为顶点的三角形和以B.O.Q为顶点的三角形相似吗?以A.O.P为顶点的三角形和以B.O.Q为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由． (2)试判断t＝2+时.以A为圆心.AP为半径的圆与以B为圆心.BQ为半径的圆的位置关系,除此之外⊙A与⊙B还有其它位置关系吗?如果有.请求出t的取值范围． (3)请你选定某一时刻.求出经过三点A.B.P的抛物线的解析式．
网址：http://m.1010jiajiao.com/timu3_id_442072[举报]
(本小题满分12分)
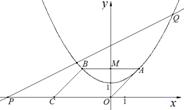
在平面直角坐标系xOy中，抛物线的解析式是y =+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上.
(1) 写出点M的坐标；
(2) 当四边形CMQP是以MQ，PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围；
② 当梯形CMQP的两底的长度之比为1：2时，求t的值.
查看习题详情和答案>>
(本小题满分12分)
在平面直角坐标系xOy中，抛物线的解析式是y =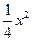
+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上.
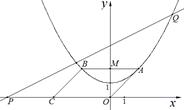
(1) 写出点M的坐标；
(2) 当四边形CMQP是以MQ，PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围；
② 当梯形CMQP的两底的长度之比为1：2时，求t的值. 查看习题详情和答案>>
在平面直角坐标系xOy中，抛物线的解析式是y =
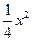+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上. (1) 写出点M的坐标；
(2) 当四边形CMQP是以MQ，PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围；
② 当梯形CMQP的两底的长度之比为1：2时，求t的值. 查看习题详情和答案>>
(本小题满分12分)
在平面直角坐标系xOy中，抛物线的解析式是y =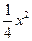
+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上.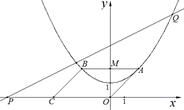 
(1) 写出点M的坐标；
(2) 当四边形CMQP是以MQ，PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围；
② 当梯形CMQP的两底的长度之比为1：2时，求t的值.
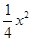+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上. 
中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知
，
，△ABC的面积
，抛物线
？若存在，求出点M的坐标；若不存在，请说明理由．