摘要:34.细心观察图形.认真分析各式.然后解答问题: (1)请用含有n(n是正整数)的等式表示 上述变化规律, (2)推算出OA10的长, (3)求出的值.
网址:http://m.1010jiajiao.com/timu3_id_441591[举报]
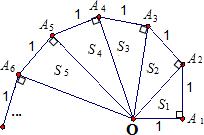 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.OA22=(
| 1 |
| ||
| 2 |
OA32=12+(
| 2 |
| ||
| 2 |
OA42=12+(
| 3 |
| ||
| 2 |
(1)请用含有n(n是正整数)的等式表示上述变规律:OAn2=
(2)求出OA10的长.
(3)若一个三角形的面积是
| 5 |
(4)求出S12+S22+S32+…+S102的值. 查看习题详情和答案>>
细心观察图形,认真分析各式,然后回答问题:
(1)直接写出OA102的长和S10的值.
(2)写出用含n(n为正整数)的式子表示上述规律OAn2和Sn.
(3)求S12+S22+S32+…+S102的值.
查看习题详情和答案>>

(1)直接写出OA102的长和S10的值.
(2)写出用含n(n为正整数)的式子表示上述规律OAn2和Sn.
(3)求S12+S22+S32+…+S102的值.
 细心观察图形,认真分析各式,然后解答问题;
细心观察图形,认真分析各式,然后解答问题;OA1=1; OA2=
| 12+12 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
OA3=
| 2+12 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
OA4=
| 3+12 |
| 4 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
…
问:(1)推算OA10的长度.
(2)推算:S10的值.
(3)求OAn的长度(用含n的代数式表示)
 细心观察图形,认真分析各式,然后解答问题:
细心观察图形,认真分析各式,然后解答问题: 细心观察图形,认真分析各式,然后回答问题:
细心观察图形,认真分析各式,然后回答问题: