题目内容

细心观察图形，认真分析各式，然后解答问题；
OA1=1；  OA2=
12+12
=
2
；  S1=
1
2
×1×1=
1
2
；
OA3=
2+12
=
3
；    S2=
1
2
×
2
×1=
2
2
；
OA4=
3+12
=
4
     S3=
1
2
×
3
×1=
3
2
；
…
问：（1）推算OA10的长度．
（2）推算：S10的值．
（3）求OAn的长度（用含n的代数式表示）
分析：（1）根据已知中OA1，OA2，OA3，OA4的长度，即可得出规律，即可OA10的长度；
（2）根据已知中数据，即可得出规律，S是分母为2，分子是根号下连续的整数；
（3）利用（1）中规律得出即可．
解答：解：（1）∵OA1=1；
OA2=
12+12
=
2
；
OA3=
2+12
=
3
；
OA4=
3+12
=
4
；
∴OA10=
10
；

（2）∵S1=
1
2
×1×1=
1
2
；
S2=
1
2
×
2
×1=
2
2
；
S3=
1
2
×
3
×1=
3
2
；
∴S10=
10
2
；

（3）根据（1）中规律即可得出OAn的长度为：
n
．
点评：此题主要考查了数字变化规律，解决本题的关键是利用数字变化得出规律．
练习册系列答案
相关题目
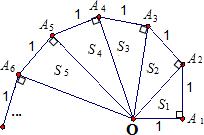精英家教网细心观察图形，认真分析各式，然后解答问题．
OA22=(
1
)2+1=2，S1=
1
2
；
OA32=12+(
2
)2=3，S2=
2
2
；
OA42=12+(
3
)2=4，S3=
3
2
…
（1）请用含有n（n是正整数）的等式表示上述变规律：OAn2=
 
；Sn=
 
．
（2）求出OA10的长．
（3）若一个三角形的面积是
5
，计算说明他是第几个三角形？
（4）求出S12+S22+S32+…+S102的值．
如图，细心观察图形，认真分析，然后回答下列问题：
（1）OA1=
 
，OA2=
 
，OA3=
 
，…，OAn=
 
；
（2）如果第一个三角形的面积用S1表示，其它依此类推．那么S1=
 
，S2=
 
，S3=
 
，…，Sn=
 
．
（3）求S21+S22+S23+…S2100的值．
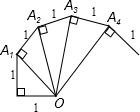
精英家教网
细心观察图形，认真分析各式，然后解答问题：
12+1=2，S1=
1
2
，(
2
)2+1=3，S2=
2
2
，(
3
)2+1=4，S3=
3
2

（1）请用含有n（n为正整数）的等式表示上述变化规律．
（2）推算出OA10的长．
（3）求出S12+S22+S32+…+S1002的值．
细心观察图形，认真分析各式，然后回答问题：
1+（
1
）2=2    S1=
1
2

1+（
2
）2=3       S2=
2
2

1+（
3
）2=4       S3=
3
2

…
（1）请用含有n（n是正整数）的等式表示上述变化规律
Sn=
n
2
Sn=
n
2
；
（2）推算出OA10的长
10
10
；
（3）S12+S22+S32+…+S102的值等于
55
4
55
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网