题目内容
 阅读理解:
阅读理解:对于任意正实数a、b,∵(
| a |
| b |
| ab |
∴a+b≥2
| ab |
结论:在a+b≥2
| ab |
| p |
| p |
(1)根据上述内容,回答下列问题:
若m>0,只有当m=
1
1
时,m+| 1 |
| m |
2
2
.(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线y=
| 12 |
| x |
(3)判断此时四边形ABCD的形状,说明理由.
分析:(1)利用已知a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2
,只有当a=b时,a+b有最小值2
,直接代入求出即可;
(2)利用S四边形ABCD=S△ADC+S△ABC,得出四边形与x之间的关系式,进而利用x+
≥2
=2
=6,得出四边形最值即可;
(3)利用(2)中结论,以及勾股定理得出AB=BC=CD=AD,即可得出四边形ABCD是菱形.
| ab |
| p |
| p |
(2)利用S四边形ABCD=S△ADC+S△ABC,得出四边形与x之间的关系式,进而利用x+
| 9 |
| x |
x•
|
| 9 |
(3)利用(2)中结论,以及勾股定理得出AB=BC=CD=AD,即可得出四边形ABCD是菱形.
解答: 解:(1)∵a+b≥2
解:(1)∵a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2
,只有当a=b时,a+b有最小值2
.
∴m+
≥2
,
∴m+
≥2,
当m=
时,
解得:m=1或-1(不合题意舍去),
故当m=1(填
不扣分),最小值是2;
(2)探索应用:
∵P为双曲线y=
(x>0)图象上的任意一点,
∴不妨可设p(x,
),
则C(x,0),D(0,
)
∵S四边形ABCD=S△ADC+S△ABC
∴S四边形ABCD=
AC×OD+
AC×OB,
=
AC•(OD+OB)
=
(|xA|+|xC|)•(|yD|+|yB|)
=
(3+x)•(
+4)
=
+2x+12
=2(x+
)+12,
又∵x>0,
>0,
∴由阅读理解中的结论可知:x+
≥2
=2
=6,
所以当x=
(x>0)时,
即当x=3时,S四边形ABCD有最小值,S四边形ABCD的最小值=2×6+12=24;
(3)此时四边形ABCD是菱形.
理由如下:
由(2)可知:当x=3时,此时点P的坐标为P(3,4),
∴AB=
=5,BC=
=5,CD=
=5,DA=
=5,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.(四条边相等的四边形是菱形).
另解:证OA=OC=3 OD=OB=4 得四边形ABCD是平行四边形,
再由AC⊥BD知平行四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
故答案为:1,2.
 解:(1)∵a+b≥2
解:(1)∵a+b≥2| ab |
| p |
| p |
∴m+
| 1 |
| m |
m•
|
∴m+
| 1 |
| m |
当m=
| 1 |
| m |
解得:m=1或-1(不合题意舍去),
故当m=1(填
| 1 |
| m |
(2)探索应用:
∵P为双曲线y=
| 12 |
| x |
∴不妨可设p(x,
| 12 |
| x |
则C(x,0),D(0,
| 12 |
| x |
∵S四边形ABCD=S△ADC+S△ABC
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 12 |
| x |
=
| 18 |
| x |
=2(x+
| 9 |
| x |
又∵x>0,
| 9 |
| x |
∴由阅读理解中的结论可知:x+
| 9 |
| x |
x•
|
| 9 |
所以当x=
| 9 |
| x |
即当x=3时,S四边形ABCD有最小值,S四边形ABCD的最小值=2×6+12=24;
(3)此时四边形ABCD是菱形.
理由如下:
由(2)可知:当x=3时,此时点P的坐标为P(3,4),
∴AB=
| 32+42 |
| 32+42 |
| 32+42 |
| 32+42 |
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.(四条边相等的四边形是菱形).
另解:证OA=OC=3 OD=OB=4 得四边形ABCD是平行四边形,
再由AC⊥BD知平行四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
故答案为:1,2.
点评:此题主要考查了函数最值问题以及菱形的判定和反比例函数的综合应用等知识,利用阅读材料得出x+
≥6是解题关键.
| 9 |
| x |

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 问栏杆多少长时,所用拉力F最小?是多少?
问栏杆多少长时,所用拉力F最小?是多少?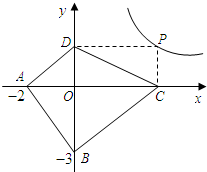 阅读理解:对于任意正实数a,b,
阅读理解:对于任意正实数a,b,