��Ŀ����
�Ķ����⣺����������ʵ��a��b����(
| a |
| b |
| ab |
| ab |
���ۣ���a+b��2
| ab |
| p |
| p |
�����������ݣ��ش��������⣺
��1����m��0��ֻ�е�m=
| 1 |
| m |
��2��˼����֤��
����ͼ1��ABΪ��ԲO��ֱ����CΪ��Բ������һ�㣬�����A��B���غϣ�������C��CD��AB������ΪD��AD=a��DB=b���Ը���ͼ����֤a+b��2
| ab |
��̽��Ӧ�ã���ͼ2����֪A��-3��0����B��0��-4��PΪ˫����y=
| 12 |
| x |
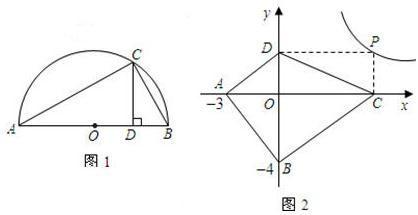
��������1��������ã�����������ӣ�ֻ������ȵ�����£�������Сֵ������������������������ֻ��1��
��2�����ɵ�D���ڵIJ�ͬλ�ã�����a��b���ڵ������������������Ӧ�Ĺ�ϵ��
��Ӧ���ݶԽ����ഹֱ���ı��ε���������Լ�����ĵ�P���������õ���Ӧ���ۣ�
��2�����ɵ�D���ڵIJ�ͬλ�ã�����a��b���ڵ������������������Ӧ�Ĺ�ϵ��
��Ӧ���ݶԽ����ഹֱ���ı��ε���������Լ�����ĵ�P���������õ���Ӧ���ۣ�
����⣺��1���ؼ������m=1����
���۷֣�����СֵΪ2��
��2���١�AB�ǡ�O��ֱ����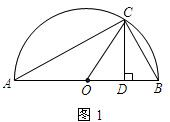
��AC��BC��
�֡�CD��AB��
���CAD=��BCD=90��-��B��
��Rt��CAD��Rt��BCD��
��CD2=AD•DB��
��CD=
��
����D��O���غϣ���OC��
��Rt��OCD����OC��CD��
��
��
��
����D��O�غ�ʱ��OC=CD��
��
=
��
����������
��
����a+b��2
����CD���ڰ뾶ʱ���Ⱥų�����
��̽��Ӧ�ã���P��x��
����
��C��x��0����D��0��
����CA=x+3��DB=
+4��
��S�ı���ABCD=
CA��DB=
��x+3������
+4����
����ã�S=2��x+
��+12��
��x��0��
��0��
��x+
��2
=6��
ֻ�е�x=
����x=3ʱ���Ⱥų�����
��S��2��6+12=24��
��S�ı���ABCD����Сֵ24��
��ʱ��P��3��4����C��3��0����D��0��4����AB=BC=CD=DA=5��
���ı���ABCD�����Σ�
| 1 |
| m |
��2���١�AB�ǡ�O��ֱ����

��AC��BC��
�֡�CD��AB��
���CAD=��BCD=90��-��B��
��Rt��CAD��Rt��BCD��
��CD2=AD•DB��
��CD=
| ab |
����D��O���غϣ���OC��
��Rt��OCD����OC��CD��
��
| a+b |
| 2 |
| ab |
����D��O�غ�ʱ��OC=CD��
��
| a+b |
| 2 |
| ab |
����������
| a+b |
| 2 |
| ab |
| ab |
��̽��Ӧ�ã���P��x��
| 12 |
| x |
��C��x��0����D��0��
| 12 |
| x |
| 12 |
| x |
��S�ı���ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| x |
����ã�S=2��x+
| 9 |
| x |
��x��0��
| 9 |
| x |
��x+
| 9 |
| x |
x��
|
ֻ�е�x=
| 9 |
| x |
��S��2��6+12=24��
��S�ı���ABCD����Сֵ24��
��ʱ��P��3��4����C��3��0����D��0��4����AB=BC=CD=DA=5��
���ı���ABCD�����Σ�
���������������������е�������������������ֻ��1������⣮�ں����������ע��ʹ��Բ�������߶����������ε������Լ������ı��ε��������

��ϰ��ϵ�д�
 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
�����Ŀ
 �����˶��ٳ�ʱ����������F��С���Ƕ��٣�
�����˶��ٳ�ʱ����������F��С���Ƕ��٣�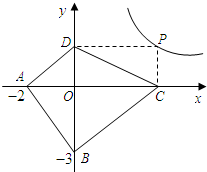 �Ķ����⣺����������ʵ��a��b��
�Ķ����⣺����������ʵ��a��b��
 �Ķ����⣺
�Ķ����⣺